なぜこの問題は良問なのか?
この問題はよく「ゆとり教育の一環で円周率を3にしようとする文科省への東京大学による反逆である」といわれます。しかし、初めに言っておくとこれはウソです。実際にはゆとり教育の下でも小学校の教科書では円周率を3.14として教えていました。
人々が「ゆとり教育では円周率が3」という誤解をし、これがなかなか解けなかった要因は大手学習塾による大々的なキャンペーン、およびマスメディアの過剰な報道にあるとされています。当時はネットの普及もそこまで進んでおらず、今よりも正しい情報を得るのが大変な時代ではあったとはいえ、学習指導要領をよく読めば「小学校では円周率は3.14として教えよ。ただし、必要があれば3にする配慮をせよ」という文科省の当初の意図が分かるはずなのです。
話を戻して、今度は円周率そのものについて考えていきましょう。もちろん円周率は3ではありません。ただし、3.14でもありません。一応こういった数字を使わずに円周率を説明すればギリシア文字を使って「円周率はπ(パイ)である」と言えるでしょう。しかし、「円周率は3.14!」という人を批判する人のうち、どれだけの人が円周率の定義を正しく言えるのでしょうか?
東京大学の数学の入試問題はこうした本当に基本的な部分を正しく理解しているかどうかが肝なのです。さて、問題は無事解けましたでしょうか?解けたという人も、考えてみてはいるけどまるで見当がつかないという人も一旦、下の解説をご覧ください。まずは、解答に至る切り口から説明していきます。
この問題を解くために
必要な考え方
初めに円周率の定義を書きます。円周率は、π=(円周)/(円の直径)で与えられます。これは知らなかった、という人がかなり多いかと思います。そうです、小学校で習った円周の公式であるL=2πrをπについて解くことで円周率の定義になるのです。
今回このことはあまり問題にはなりませんが、このようなことをきちんと抑えられているかどうかは東大入試の肝です。余談ですが、この円周の公式の右辺をrについて0からrまで積分するとπr^2となり、半径rの円の面積になります。
それではいよいよこの問題の解法を説明します。この問題では「円周率が3.05以下だと何が困るか」を考えれば答えに辿り着きます。なるほど、そういう意味ではこの問題を「ゆとり教育への風刺」と捉えても良さそうですね。
こうしたことを考える時は簡単な具体例から入るのが基本です。プロの数学者であってもそうしてます。今回は単位円に内接する正六角形を考えましょう。この正六角形は下の図のように、一辺の長さが1の正三角形が6つ集まったもの(市販の6切れに分かれた円形チーズに似てますね)と見ることができます。
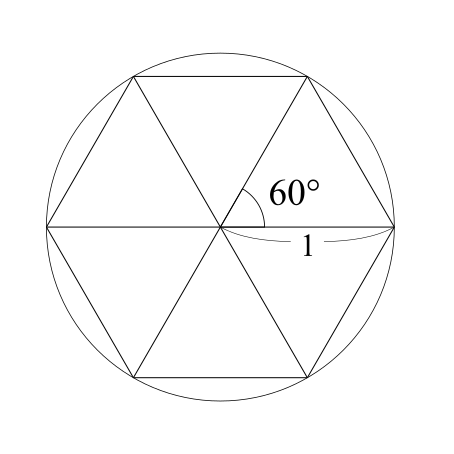
するとこの正六角形の周の長さは6になります。次は単位円の円周を考えましょう。これは先ほどの式から2πとなりますが、ここでπ=3を代入してみます。すると単位円の円周は6になります。もうお気づきかと思いますが、そうです。仮に円周率を3にしてしまうと、単位円の円周とそれに内接する正六角形の周の長さが一致するという、明らかに直観から外れた結果になってしまうのです……!
同じ2点間を結ぶなら直線で結ぶのが最短に決まっています。なのでこの図形を見るだけで2π>6、すなわちπ>3がわかります。……さて、突破口は見えましたか?そうです。これからあなたにやっていただく操作は、このまま正〇角形の数字をどんどん大きくして、π>3.05がわかるまで試してみることなのです!
まだ解けていない、という方はここで一旦下にスクロールするのをやめ、実際に紙とペンを用意して解いてみましょう。流れは先ほどの論証と同じですが、内接する図形はかなり複雑なものになります。そうなると少しだけ計算が大変ですが、東大を受けるなら解けて当然のレベルです。確実にビタッ!と合わせましょう。
解答(円周の長さを用いる方法)
解答はこちらになります。ここでは正十二角形を使っています。
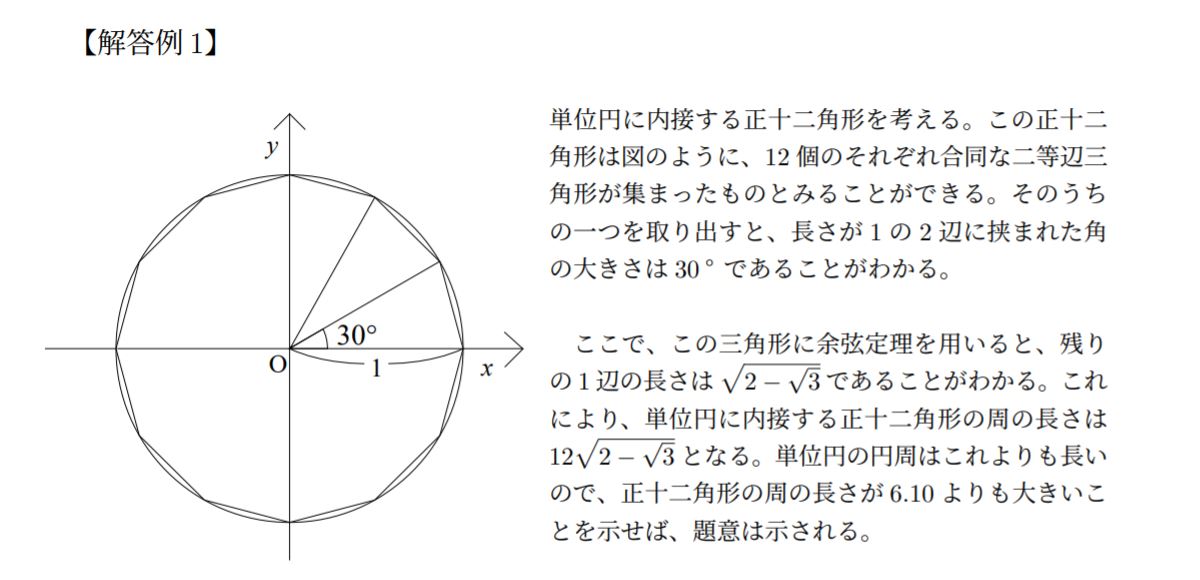

どうでしたか?この解答では二重根号を公式通りのやり方(覚えていますか?)で外しましたが、本番でド忘れした場合は両辺を2乗して解決できます。その場合はπの2乗を3.05の2乗と比較することになるので、そこだけは間違えないようにしましょう。
また、√2と√3の値の評価はきっちりとやりましょう。πの値が未知なのに同じ無理数の√2と√3の値が既知というのも変な話のように思えますが、流石にそれらの値は使っていいと思います。√2=1.41421356…と√3=1.7320508…は東大受験生なら誰でも知っていることかと思いますが、今回はあえて√2は1.415以下、√3は1.732以上という扱いをしました。なぜでしょう?
その答えは誤差の問題があるからです。あまり位の多すぎる数字を使っても計算を煩雑にするだけなので最小限の数字で堅実にやりたいところですが、そこで例えば√2≒1.41、√3≒1.73のように計算式を書き直してしまうと、この段階で有効数字の関係が滅茶苦茶になり、実際の計算結果と大幅にズレることになるためです。
今回は√2については有効数字3桁で√2≦1.41としてもよいですが、√3に関しては引き算があるので√3≧1.732としなければ減点です。最終的には3桁の数字で6.10と比較できるようにしましょう。
ちなみに、この問題は本番での出来はかなり悪かったようです。このレベルの正答率であれば答えまでの筋道がそれらしく書けているだけでかなりの得点を期待できますが、簡単な問題での証明の粗さは確実に合否に響きます。例えば先ほどの√2と√3の評価の話にしても、ここをサボるだけで半分ぐらいの点数を持っていかれる、というようなことは十分ありえる話です。
別解・面積を比較する
数学の問題を解く際は、時間に余裕があれば別解がないか探してみましょう。「もう既に解き方見つけたのに、なんでわざわざそんなことを?」と思われる受験生も多いかと思います。確かに、別解探しをすると1つの問題にかかる時間はその分長くなり、一見非効率的です。
しかし、別解を探すことは数学を勉強する上ではとても大切なことです。複数の別解を試すことで、数学を学ぶ上で必要な視点をたくさん得ることができます。受験の世界でも、様々な方法を頭の中に準備できるようになり、初見の問題でもすらすら解ける確率が上がるという明白なメリットがあるのです。
この問題は単位円とそれに内接する図形の面積を比較することでも解くことができます。具体的には正24角形を用い、面積比較を行うことになります。

こちらの方が計算は簡単に済みそうです。余弦定理より三角形の面積公式の方が計算は楽であることが多いです。本番では1%程度、この解き方を試した受験生がいたそうです。
東大入試の数学はこう攻めよ
~この問題から分かること~
ここからは特に東京大学の入試の数学を解く上で重要なことについて話していきます。東京大学を目指している方はもちろん、他の大学を目指しているという方にも大切なことを書いておりますので、ぜひ最後までお読みください。
今回の問題を解いてて恐らく多くの方が思ったことは、どの図形であればπ>3.05を示せるのか?という図形を探す作業が結構しんどい、ということだと思います。一番計算が容易な正方形ではπ>3、ルートが見えてちょっと計算がしんどくなる正八角形でもπ^2>9.28(3.05^2の値は9.3025)と、なかなか思うような結果が得られません。
例え解法が見えても、それを答えに起こす作業も一苦労なのが東大入試です。なかなかすんなりとはいきません。先ほど、この問題の解答を作るための計算はできて当たり前のように書きましたが、その理由は東大の数学はこのような面倒な作業の連続な上、時間の制約も文科は100分で4問、理科は150分で6問というとても厳しいものだからなのです。
入試そのものの詳細はこちらの東大入試解説ページをご覧いただくとして、東大の数学がなぜこのような出題であるかということを話します。その理由はこれが「数学者としての適性が見られるテスト」になっているからです。こんな退屈な作業を繰り返すだけのもののどこがそうなんだ、と思われるかもしれませんが、この単調な計算や具体例の検証の繰り返しが数学をする上ではとても重要なのです。
東大数学科の某教授は「数学を考えようと思って考えるうちは二流である。無意識に夢の中でも考えられるようになって初めて一流である」などと言ったといわれています。発言自体の真偽のほどは定かではありませんが、これは数学という学問の特徴をよく言い当てているといえます。数学では天才的な発見をする閃きも大事ですが、目の前の単調な計算や検証作業をずっとやり続けられる根気強さの方がずっと重要になるのです。
東大の数学はこのために計算量や具体例の検証の量がとても多くなっています。この円周率の問題1つ取ってもそうです。そしてこの傾向は他大でも大して変わりなく、計算や検証を愚直に行う根気強さはとても重要であることがわかります。
ですから、大学入試の数学を、特に東大入試の数学を攻略するためには、日頃から計算練習を重ね、鍛えていくことがとても重要なのです。とはいえ、この程度であれば一人でできる、という方も多いかもしれません。
しかし、一人での勉強は得てして心細いものです。大学入試の直前期では1日10時間の勉強は当たり前で、東大の理科三類ともなれば、1日15時間やるのは当たり前の世界です。毎日それだけの長い時間、誰からの大した支えもない状況のもとでは心細くなって、自分が何のために今勉強をしているのかすらも分からなくなります。そのうちにライバルには水をあけられ、当初夢見ていた志望校への合格からはすぐに遠ざかってしまいます。
そうならないためにはどうすればいいか?答えは単純、心強い仲間を見つけることです。そして、心強い仲間とは例えば、かつて東大の数学を突破するために必死に勉強し、その結果見事東大合格を勝ち取った、現役東大生の人たちです。
東大家庭教師友の会では、このような現役東大生の家庭教師をご紹介できます。選び抜かれた優秀な教師の指導が比較的安価に受けられるほか、生徒様ご自身で細かい条件から先生を指名できますし、日々の訓練に必要なモチベーションの管理も徹底的にいたします。東大に合格したい、数学をもっと得意にしたいという生徒様を、友の会は全力でサポート致します。
あわせて読みたい|大学数学の良問を解説!
東大家庭教師友の会の特徴
当会には、東大生約9,700名、早稲田大学生約8,500名、慶應大生約8,000名をはじめ、現役難関大生が在籍しています。
生徒様の憧れとなる教師のご紹介と、安心・充実のサポート体制で、生徒様の目標達成に貢献します。
大学受験数学の指導ができる家庭教師の紹介
上記は在籍教師の一例です。他にも様々な経歴の教師が在籍しています。ご希望の条件の教師が在籍しているかは無料でお探しできますので、まずはお気軽にお問合せください。
オンラインでの指導も可能です
東大家庭教師友の会オンラインHPを見る



















