画像の問題は1999年の一橋大学で出題された、入試業界でも有名な問題です。この記事では「この問題はどのように解けばいいのか」「どこに引っ掛けがあり、それを見抜くにはどうすればよいのか」を深掘りしていきます。
まずは画像の問題にじっくり当たって解いてみましょう。解けたら以下の解説を読んで合っているか確かめましょう。もちろん、まったく解法が見当がつかない、15分ぐらい考えてみたけどわからない場合でも下の解説に進んでかまいません。
※今回の問題はかなり難しいです。図形問題が苦手な方はご注意ください。
目次
今回の問題を解くために
必要な考え方
まずは問題文が求めている状況はどういうものなのかみていきましょう。今回のような図形問題は問題文が指すものを具体的に書いていくとわかりやすいです。
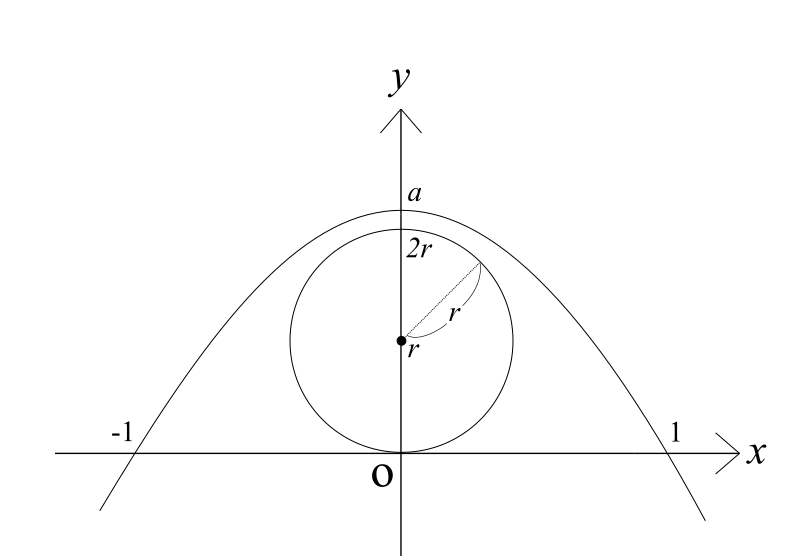
まずは上の図を見てください。「x軸と放物線y=a(1-x^2)に挟まれた範囲にあり、なおかつx軸に接している円」を描くとこのようになります。図ではaが1よりも小さいのですが、aについては後で0より大きい範囲で様々に動かして考えます。
ここで注意することは円を「aを固定した状態で」最大にするということです。なぜここでaを固定するのでしょうか?それはaが動くことは放物線が動くことと同義であり、放物線に束縛された円の大きさを考えている最中に放物線に動かれては困るからです。
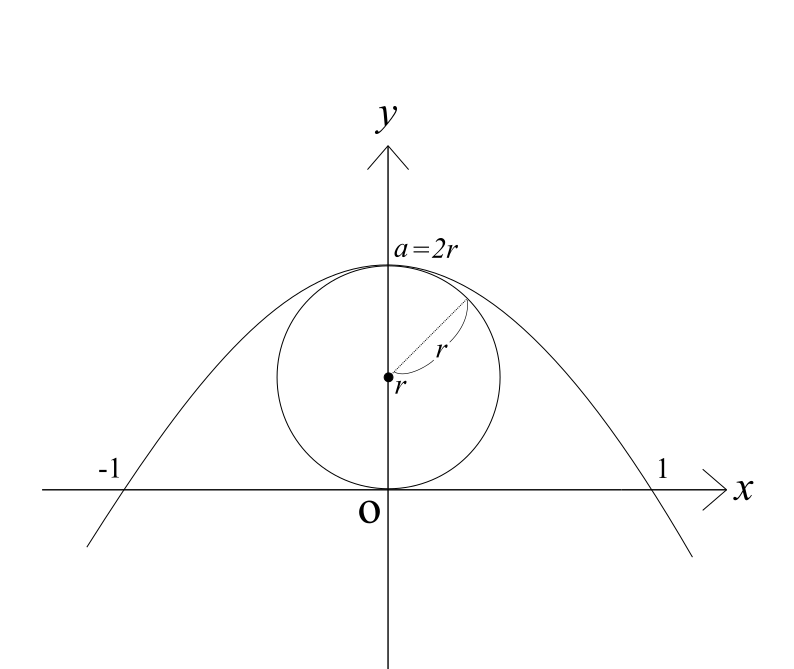
したがって、a<1のまま円の大きさを最大にしました。その結果が上の図になります。このときa=2r(rは円半径)となり、(0,a)の1点のみで円と放物線が接します。

a>1の場合は上のように2点で接します。このように、円の大きさが問題文に示された条件下で最大になるときは、円は放物線に1点または2点で接します。
さて、放物線が円に接するということは、円と放物線の交点を(s,t)として、$$s^2+(t-r)^2=r^2 かつ t=a(1-s^2)$$という関係が成り立ちます。sとtのどちらか一方を消せば、未知の変数が減って解答を書きやすくなります。
ただしそれだけでは解答を書くには足りません。上の2式のみでは、例えば以下の図のように、「円と放物線が3点または4点で交わる場合」であっても適用できてしまうためです。
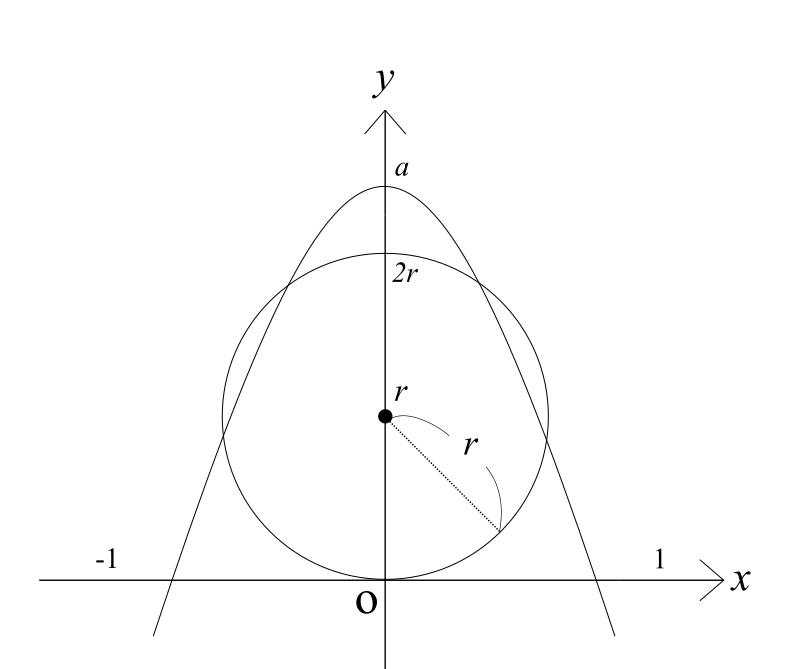
この場合でも上の2式は適用できてしまいます。そのため、上手く1点か2点だけ接している状態に絞れるように工夫する必要があります。
この先の方針は主に2つに分かれます。「上記2つの式からsを削除してtについての2次方程式を作り、その重解を利用する」か、「放物線と円の中心の最短距離を求め、これをrとする」かの二択であり、これは考え方の違いです。今回はこの2つの場合の解答を作成します。
重解を利用した解答
重解を利用する解答のポイントは「y座標に注目する」ことです。先ほど見ていただいた画像のうち、2点で接しているものに注目します。すると、2点のy座標が同じであることがわかります。
ここで接点のy座標tについての2次方程式をここまでに書いた式から立ててみましょう。$$t^2-(2r+\frac{1}{a})t+1=0$$ この式が出てくるならOKです。これをtについて解くと、$$t=\frac{2ar+1\pm\sqrt{(2ar+1)^2-4a^2}}{2a}$$ となります。しかしこれだけでは何も分かりません。ここで「1点が2点で接するときのy座標は共通である」ことに注目します。これはすなわちこの方程式を満たすtがただ1つであることを示します。
ここからは判別式をDとしてD=0の式をrについて解きます。あとはaの値によって場合分けすれば終了です。ここからは実際の解答となります。


この解答を書くときの引っ掛けポイントは「D=0で必ずしも円と放物線は接しない」ということです。どうして?と思われた方は以下の画像を見ればわかると思います。
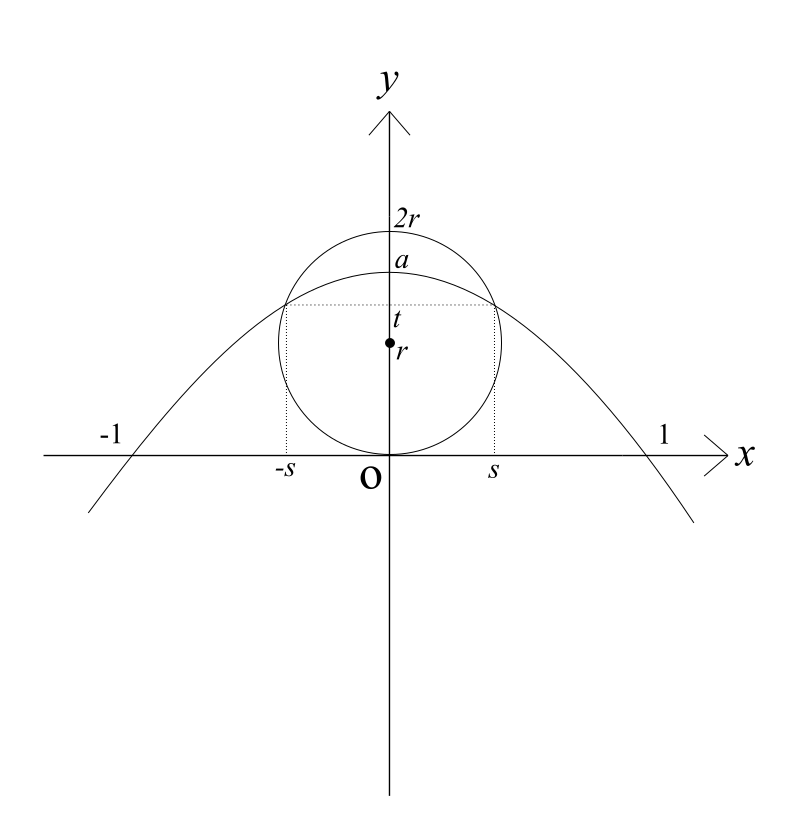
画像ではたしかに円と放物線の交点のy座標はtで共通しています。しかし、「接して」はいません。したがってこのような場合を排除して考える必要があり、a≦1がこれに該当します。図を書くとわかりやすいでしょう。
これを見抜くためには「必要十分条件を常に考えながら解き進める」ことを意識しましょう。「円と放物線が接するには高々2つのy座標が等しければよい」ということは正しいです。しかし、いま見たように逆は正しくないため、この点に気を付けながら冷静沈着に解答を作成する必要があります。
円の中心と放物線の
最短距離を求める解法
今回の問題を見て「円の中心と放物線の最短距離がrになればよいのでは」と気付いた方は多いと思います。実際、過去の大学入試では似たような問題をこの解法で解くように指示したケースがあるそうです。ただし、少々落とし穴があります。
最初に言います。点と直線の距離の式は使用しないでください。筆者もはじめは点と直線の距離の公式を使って解こうとしました。しかし、あまりに式が複雑になってしまい、諦めたという経緯があります。
どうすればよいのかをここから解説します。まずは放物線上の任意の点をPとおき、さらに円の中心と点Pの間の距離をdとおいてください。そして、Pの座標を(s,t)とし、-1<s<1であるとしましょう。すると、tには自動的にt>0の条件がついて、$$d^2=s^2+(t-r)^2$$とすることができます。dの二乗が最小値をとるときに、d=rとしてrを求めればよいのです。
式変形などの方法は先ほどの解法に同じです。では解答を書きます。


一部の不等号にイコールが付きましたがa=1のときはどちらに代入しても1/2なのでこれでもOKです。こちらはただの二次関数の最大最小の問題になるので、高校1年生でも解けます。当時は苦労したような内容でも入試の段階では朝飯前で解けなければなりません。
本番で引っ掛けを
見抜けるようになるために
今回見ていただいた引っ掛けを見抜くコツのひとつに「必要十分条件に気をつける」というものがありました。これは数学の問題を解く上での基本中の基本です。
式を変形したり、考える変数を変えたりするときには毎回「AからBがいえていたとしても、BからAは果たしていえるのか?」というふうに小休止する必要があります。
また、本文中ではあまり強調しませんでしたが、今回のような図形問題は「図を描いて考える」ことが基本になります。頭の中だけで考えると分かりにくいことも、図を描いていくことで的確にイメージできるようになります。とにかく描くことです。
このような工夫をすれば引っ掛けに対処できるようになります。そして、どのような問題にもこのような工夫ができれば、ほとんどのミスは防げます。
そのためには多くの問題を解いていくことが何より重要なことです。ここで東大家庭教師友の会所属の学生家庭教師の力を借りることで、数学攻略に向けて大きくブーストをかけられるようになります。
友の会所属の家庭教師の強みは全員が難関大在籍の現役学生家庭教師であることです。彼らは実際に難関大の整数問題、そして数学を攻略するためのノウハウを持っているだけでなく、大学受験を経験して日が浅いことから、親身になってあなたのサポートをすることができます。
また、全員が通過率20%以下の厳しい審査を通っています。そのため、生徒様のサポートを卒なくこなせる学力だけでなく、立派な人格まで備えた家庭教師をご紹介することが出来ます。大学入試の数学を攻略したい、第一志望校に合格したいあなたの背中を、私達友の会は全力で押します!
大学入試の数学対策は
友の会の家庭教師で決まり!
友の会の3つのメリット
特に数学を頑張りたいあなたへ向けて我々友の会が提供できるメリットは大きく分けて以下の3つになります。まずは一度、お読みください。
①数学が大得意な先生が教えてくれる!
友の会には京大、東大、大阪大をはじめ40,000人以上の難関大生が在籍しています。それだけ多くの家庭教師がいますから、数学を大得意とし、その数学力で入試を勝ち上がった先生も多く紹介できます。
それだけではありません。友の会の家庭教師は全員採用率20%以下の厳しい審査を通過しています。そして、教師に希望する条件で細かく絞り込みができます。もし相性が悪いと感じられた際には教師を交代させていただくことも可能です。
②モチベーションを徹底管理!

東大家庭教師友の会の教師は、生徒様の学習が成果につなげられるように、授業以外にも充実した学習サポートを行なっております。
日頃の計算練習や苦手克服のための問題演習など、数学の勉強はとにかく時間のかかる地味な作業も多いです。そのような場面でもモチベーションを失ってしまわないよう、友の会の家庭教師が徹底的にサポート。お悩みにも親身になってお応えできます。
③かかる料金は5つだけ!
東大家庭教師友の会では、ご入会時に入会金が発生します。月々のお支払いは、コースに応じた授業料、交通費、学習サポート費の合算になります。
授業を受けた時間数に応じてご請求額は変わり、指導回数や時間を臨機応変に変更することが可能です。
他社の家庭教師とはどう違う?
次に、東大家庭教師友の会と他社の違いを紹介します。東大家庭教師友の会の家庭教師は他社の家庭教師と比べて、「生徒様にぴったりの家庭教師を派遣できる」こと、「質の高い授業をリーズナブルに受けられる」ことが大きなメリットです。具体的に見てみましょう。
①生徒様にぴったりの家庭教師!
家庭教師は生徒様との相性がすべてです。どれだけ指導能力の高い家庭教師であっても、生徒様との相性がよくなければ、その能力を十分に活かすことはできません。その点、友の会は安心です。東大家庭教師友の会は体験授業(初回無料)によって教師との相性をチェックでき、もし合わないと思った場合はいくらでもチェンジできます。
教師の条件は出身校や在籍大学など、細かい条件で事前に指定することができます。いつ指導して頂くかもご家庭様でご自由に決めて頂けます。また、東大家庭教師友の会は原則すべての案件に立候補制を採用しているので、どの先生も熱意に溢れています。
さらに、東大家庭教師友の会の最大の特徴は「全員学生家庭教師であること」です。これは、生徒様と相性のよい家庭教師が見つかりやすいことを示しています。生徒様と歳が近く、価値観や趣味を共有できる可能性がプロの家庭教師よりも高いのです。
同業他社の場合ですと、例えばプロ家庭教師は経験豊富ですが、歳は生徒様から離れており、委縮してしまうかもしれません。教師の在籍数が少ないところではそもそも生徒様に合う教師が見つからない可能性すらあります。そして、本来生徒様と教師の相性をチェックして頂く最もよい機会である体験授業にそれ専用の人材を派遣してくる業者もあるようです。この点には十分注意する必要があります。
②明瞭な料金制度・高いコスパ
友の会の授業は難関大所属の家庭教師による質の高いものでありながら、コスパよくご利用いただけます。なぜなら、友の会では広告宣伝費などの諸費を極力安く抑えているからです。さらに、ご家庭様から頂く料金の大部分が教師の給与となるシステムも確立していますので、給料が安いことが原因で教師が積極的な指導をしてくれない、といったこともございません。
また、東大家庭教師友の会では後払い制度を採用しています。さらに、月謝制ではなく、その月の指導日数および指導時間により料金を計算させて頂いています。これにより、毎月指導を受けた分だけ、確定後にお支払いして頂けるような仕組みを整えております。
東大家庭教師友の会は先ほども見て頂いたように料金体系をあらかじめ明示していますが、一度問い合わせるまで料金を明示してくれない業者もあります。同業他社との詳細な料金比較は【30社】家庭教師料金を徹底比較!をご参照ください。
以上の点から、東大家庭教師友の会は他社と比較してもなお信頼できる家庭教師サービスであることがご理解いただけたかと思います。
大学入試の数学対策におすすめの家庭教師
以下に紹介する家庭教師はすべて現役の大学生であり、合格経験をもとにした質の高い指導をすることができることを当会が認めた優秀教師です。もっと多くの家庭教師の情報を見たい方は教師情報検索からどうぞ。
 上杉 上杉 |
上杉先生 |
 |
||||||
| お問い合わせ番号 | 848174 |
 |
上杉先生 |
 |
||||||
| お問い合わせ番号 | 848174 |
| 所属大学 | 一橋大学 |
| 出身高校 | 西大和学園高等学校 |
| 指導期間 | 2023年3月まで |
| 指導科目 | [小]国語,理科,社会,算数,英語
[中]国語,数学,理科,社会,英語 [高]世界史,倫理,古文,地理,政経,文系数学,日本史,漢文,現代文,現代社会,英語 |
| 意気込み | 担当の生徒様および保護者様の意向に合わせ、生徒様のモチベーションを維持しながら、志望校の合格、成績の向上に向けたより良い学習プランを提案して参りたいと思います。 具体的には、学習につながるようなエピソードや知識の背景となるようなお話を通して、主体的な学びにつながるような指導法を実行していきたいです。 |
 |
宮田先生 |
 |
||||||
| お問い合わせ番号 | 865741 |
 |
宮田先生 |
 |
||||||
| お問い合わせ番号 | 865741 |
| 所属大学 | 一橋大学 |
| 出身高校 | 浦和西高等学校 |
| 指導期間 | 2023年3月まで |
| 指導科目 | [小]国語,理科,社会,算数,英語
[中]国語,数学,社会,英語 [高]倫理,古文,小論文,文系数学,日本史,漢文,現代文,英語 |
| 意気込み | 勉強、1人でするのは不安です。そんな生徒様と共に寄り添って、サポートさせていただきます。一緒に頑張りましょう! |
 |
飯塚先生 |
 |
||||||
| お問い合わせ番号 | 723822 |
 |
飯塚先生 |
 |
||||||
| お問い合わせ番号 | 723822 |
| 所属大学 | 慶應義塾大学 |
| 出身高校 | (県立)浦和高等学校 |
| 指導期間 | 2022年3月まで |
| 指導科目 | [小]国語,理科,社会,算数,英語
[中]数学,理科,社会,英語 [高]文系数学,日本史,英語 |
コースごとのご料金をチェック▶コースごとのご料金をチェック▶
| 意気込み | 生徒様に心を開いてもらい、良い関係を構築し指導していきます! |
料金
東大家庭教師友の会では、ご入会時に入会金が発生します。月々のお支払いは、コースに応じた授業料、交通費、学習サポート費の合算になります。
授業を受けた時間数に応じてご請求額は変わり、指導回数や時間を臨機応変に変更することが可能です。
お問い合わせはこちら
以上の一橋大入試の数学の良問解説はいかがでしたか?友の会の家庭教師の指導に興味を持った方はまずは一度お問い合わせください。
以下は電話、およびWEB上でのお問い合わせのリンクになります。対面での指導を希望される方は派遣可能エリアをご確認の上、こちらからお申し込みください。
派遣可能エリア外にお住まいの方でも授業をお受けいただけるよう、オンライン指導もご用意しております。
「家庭教師は欲しい、でもコロナが怖い!」という方にもおすすめのオンライン指導をご希望の方は下記のリンク先をご覧ください。
他の入試数学の問題について見る
東京大学
円周率は3.05より大きい(2003年) ~ゆとり教育への挑戦状?~
初代・閻魔の唇問題(1954年) ~閻魔が笑えば赤門は開く~
京都大学
剰余と数値計算(1999年) ~自分の得点を自分で決められる?~
tan1°は有理数か?(2006年) ~史上”最短”の入試問題~
東京工業大学
数列を割り切る素数(1986年) ~答えはすぐに分かるけれど~
同様に確からしくない確率の問題(2008年) ~いびつなサイコロ~
一橋大学
円と放物線(1981年) ~引っ掛けポイントを見抜くには?~
大阪大学
公式の証明(2013年) ~公式は証明してから使おう・阪大編~
神戸大学
対数の応用問題(1998年) ~盲点の桁数、その攻略法~
三角形の面積(1977年) ~解けなかったら落ちる?~