画像の問題は1999年の大阪大学で出題された、入試業界でも有名な問題です。この記事では「この問題はどのように解けばいいのか」「どのようなアプローチで攻略できるのか」を深掘りしていきます。
まずは画像の問題にじっくり当たって解いてみましょう。解けたら以下の解説を読んで合っているか確かめましょう。もちろん、まったく解法が見当がつかない、15分ぐらい考えてみたけどわからない場合でも下の解説に進んでかまいません。
目次
今回の問題を解くために
必要な考え方
読者の皆様は今回の問題文を見てどう感じられましたか?「長すぎる!」や「何を言っているのか分からない!」などの感想が多いことだろうと思います。
問題文が長い場合は冷静に一つ一つの要素に分解して問題文を読み進めましょう。そうすることで比較的簡単に解けることが多いです。逆に3行以内に終わる短い問題の方が難しい、ということもしばしばあります。
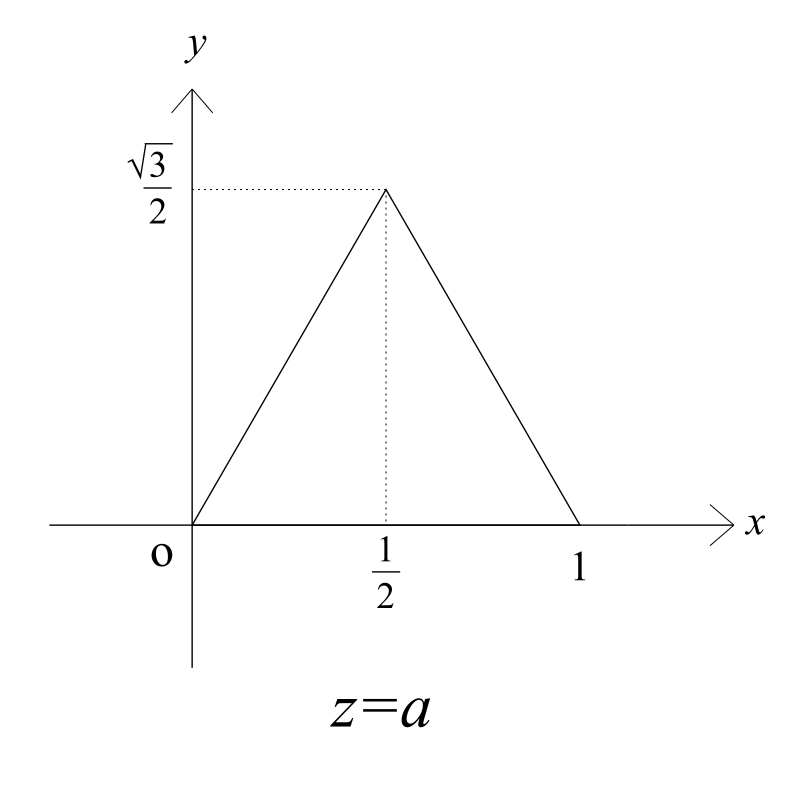
まずは立体Kの切り口を考えます。問題文から、立体Kの切り口はどのようなz=aで切っても以下のような正三角形になると考えられます。
次に立体Lの切り口を考えます。Kと同様で、どのようなy=aに対しても以下のようになります。
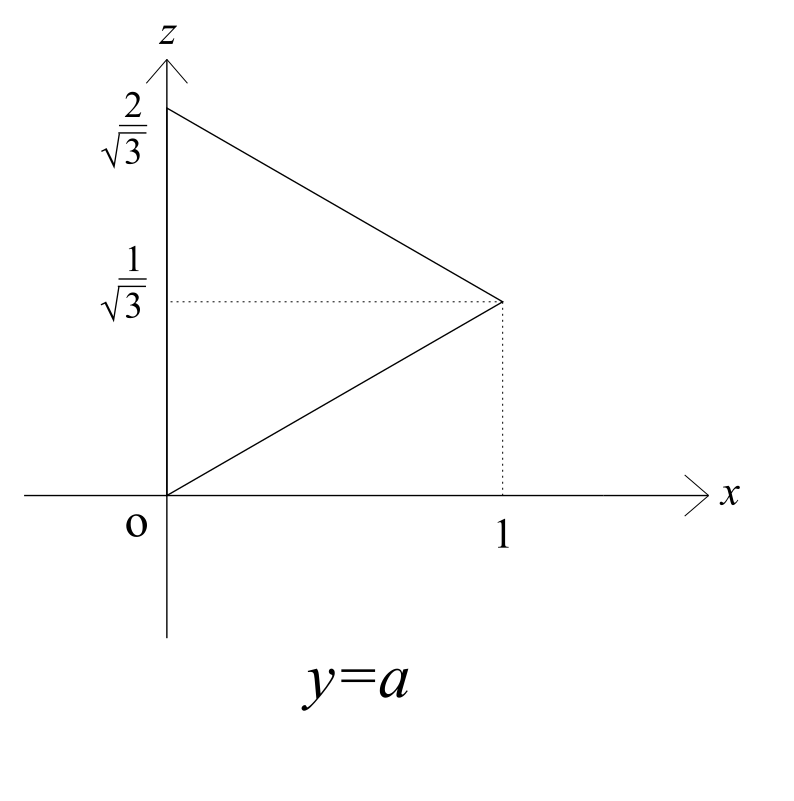
このような図形をそれぞれz=a、y=aに対して切り口として持つので、KとLの共通部分は以下のようなものであることがわかります。

図中灰色に着色された立体がKとLの共通部分です。わかりづらいですが、四角錐になっています。この部分の体積を求めるのが今回の目標です。
……しかし、これを単なる図形の問題として考えるのはかなり難しいです。よって今回は純粋な図形的アプローチを回避して、なるべく計算ずくでどうにかする方法を2つ紹介します。
今回の解法は入試本番の数学の問題を解くにあたって必ず習得するべき解法といっても過言ではありません。本番で緊張しているとなかなか頭が幾何的なアプローチをするように働いてくれない一方で、計算は落ち着いてできるからです。
積分計算による解答
このような立体の体積を求めるにあたって最も簡単な手法が積分計算を用いる方法です。この方法の合言葉は「切って足す」です。まずは下の図をご覧ください。
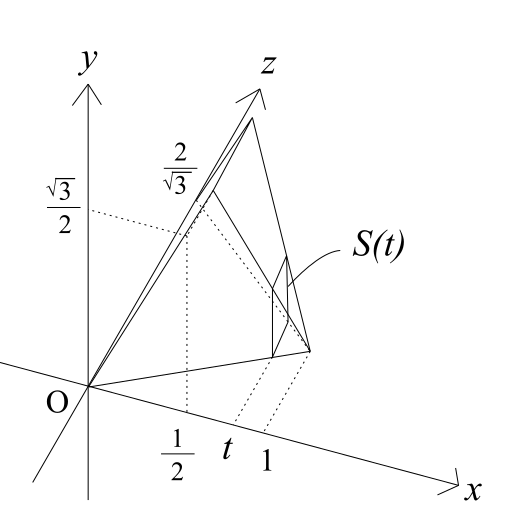
これは先ほど示した四角錐を横倒しにして考えやすくしたものです。まずはこの平面をx=tで切り、その切り口を考えます。
なぜこのようなことをするのか?そう思った人はとりあえず、この切り口S(t)をとても薄い長方形の板だと考えましょう。そしてこのtの値によって大きさを変える極薄の板をt=0からt=1まで重ねていったとき、元の四角錐になる、という説明ができます。
この「重ねていく」操作に該当するのが積分です。すなわち、求める立体の体積をVとおいたとき、これは$$V=\int_0^1 S(t) dt$$と計算できるのです。つまりS(t)を求めてしまえばあとはそれを積分するだけなのです。切り口は以下のようになります。
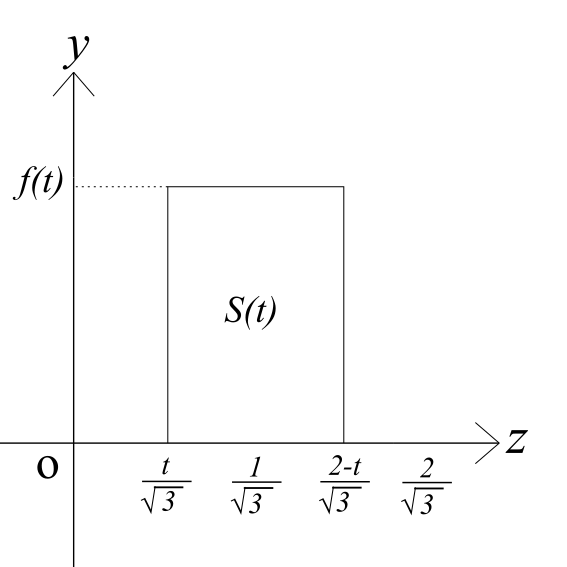
この切り口はx=tでの切り口ですので、形状はイメージです。ただし0≦t≦1では必ず長方形です。四角錐の図からy軸方向の辺の長さf(t)は$$\sqrt{3}t \quad(0 \leq t \leq \frac{1}{2} ) \\ \sqrt{3}-\sqrt{3}t \quad(\frac{1}{2} \leq t \leq 1)$$となり、z軸方向の辺の長さは$$\frac{2}{\sqrt{3}}(1-t)$$となります。すなわち、$$S(t)=f(t)\frac{2}{\sqrt{3}}(1-t)$$となるので、あとは以上の式を先ほどのVの式に入れて積分するだけです。解答は以下です。
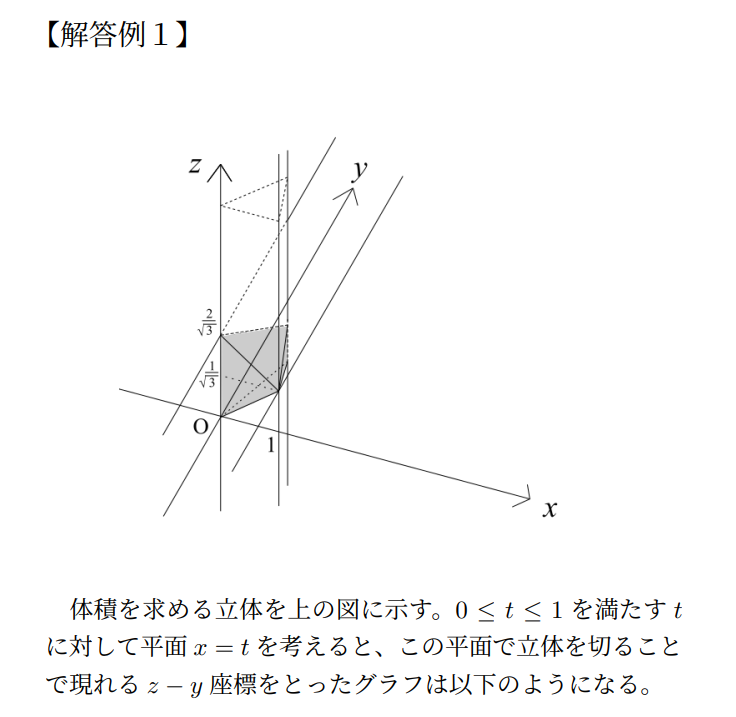
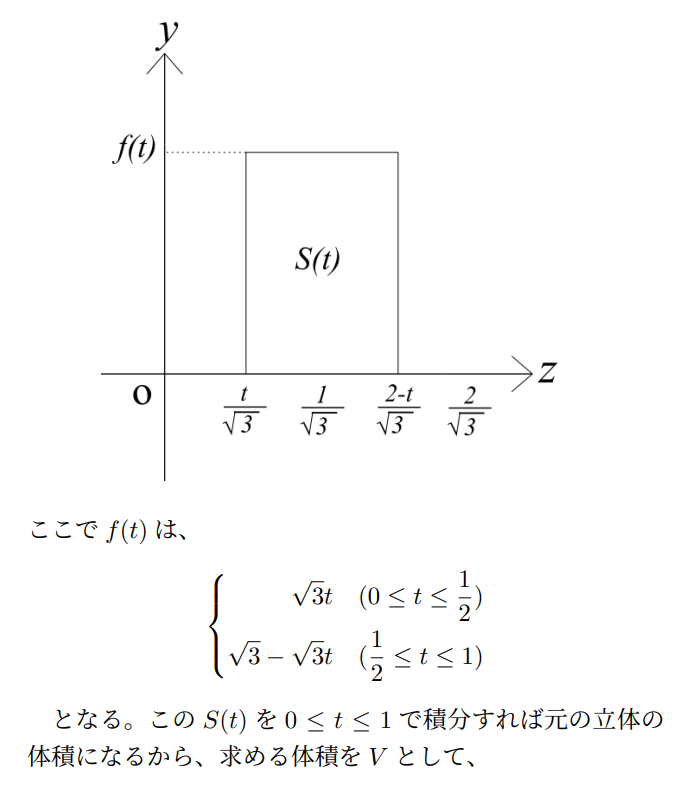
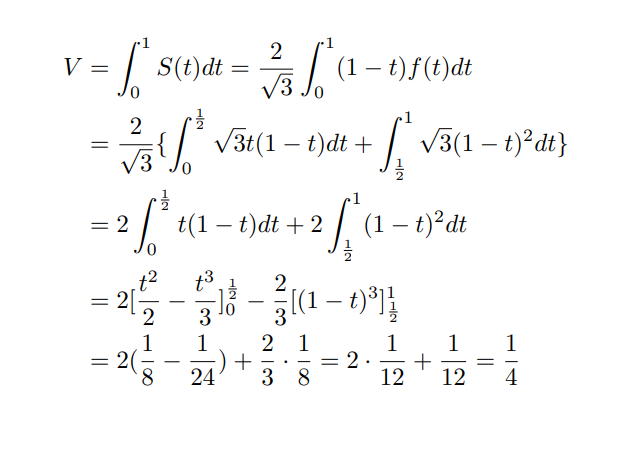
あれほど難しそうだった問題も蓋を開けてみれば計算は簡単、答えもシンプルに収まるサービス問題になってしまいました。「積分計算で体積を出す方法を知っているかどうか」が明暗を分けると言えるでしょう。
閑話休題・大学の数学への招待
計算ずくでどうにかする「もうひとつの方法」を紹介する前に、ここで少し大学の数学の内容を紹介します。
「え、今からやるの?」と思われるかもしれませんが、今回紹介する内容は入試の問題を解く上でも有用な知識です。さらに大学の入学後に待ち構えている難しい数学の単位も取りやすくなります。
ただし、今回の解答での立ち位置は考え方の骨組み作りと検算にとどまり、解答上に「外積」などの用語を直接出すことを控えながら書くこととなります。ですので、読み飛ばしたい方はこちらから次の章に移ってください。


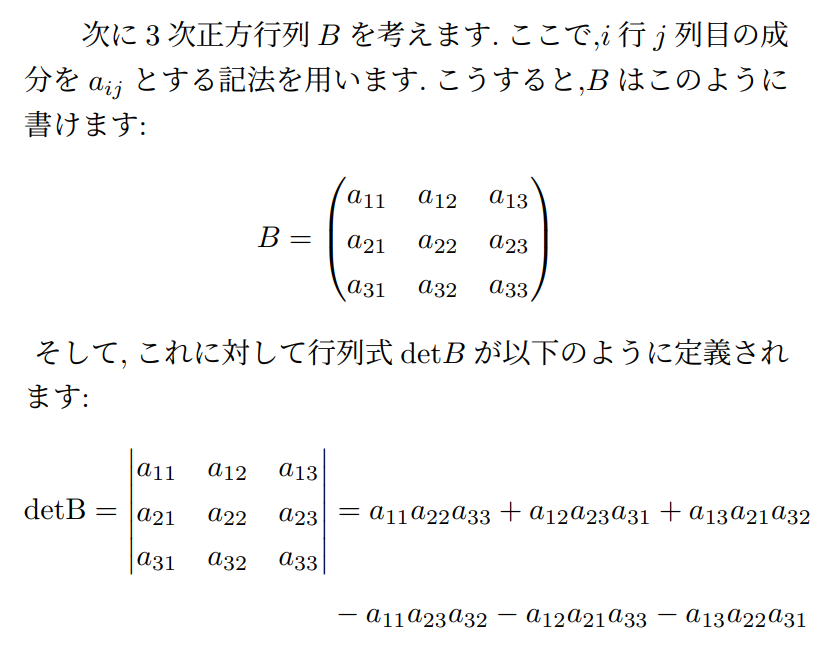
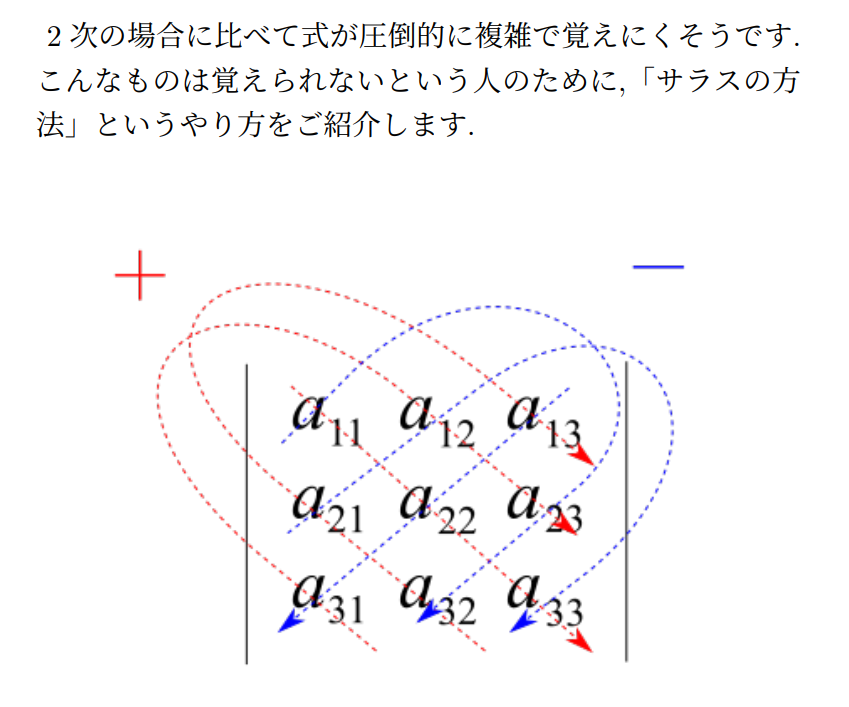

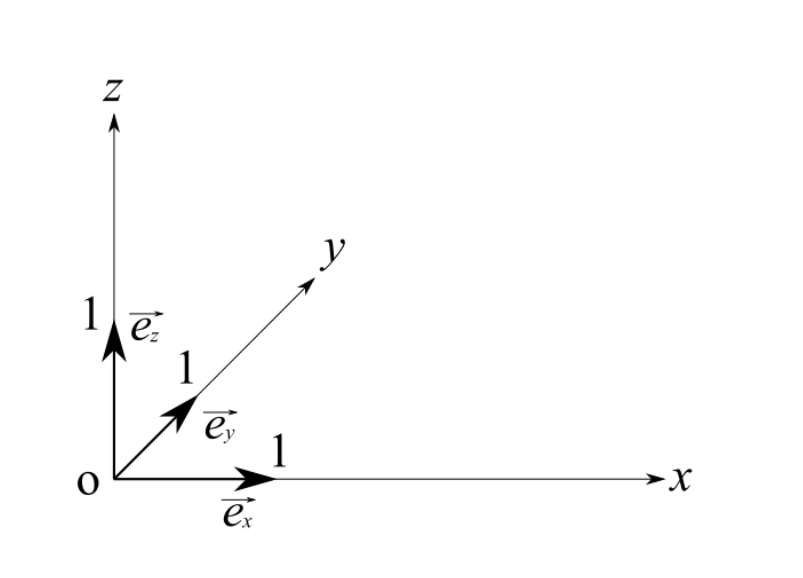

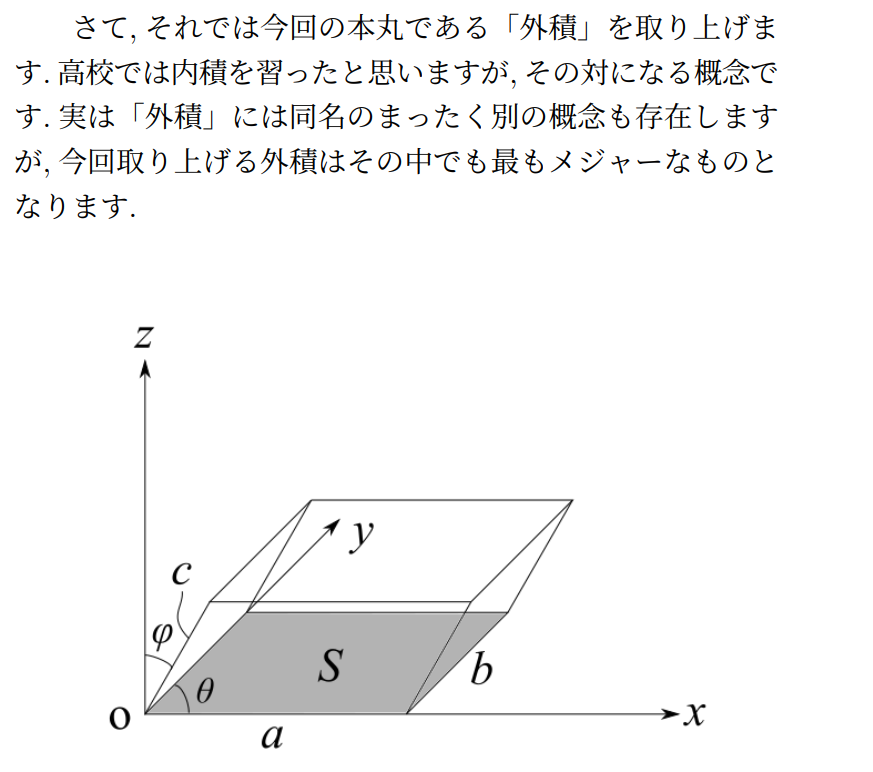








平行六面体を用いた解答
それではここから「衝撃的な解答」をお見せします。この解答はかなりロマン要素が強いので、本番であれば先ほどの積分計算による解答を使うべきでしょう。
それでは解説に入ります。まず、任意の三角錐(四面体)は平行六面体の中に入れられるということはご存知ですか?
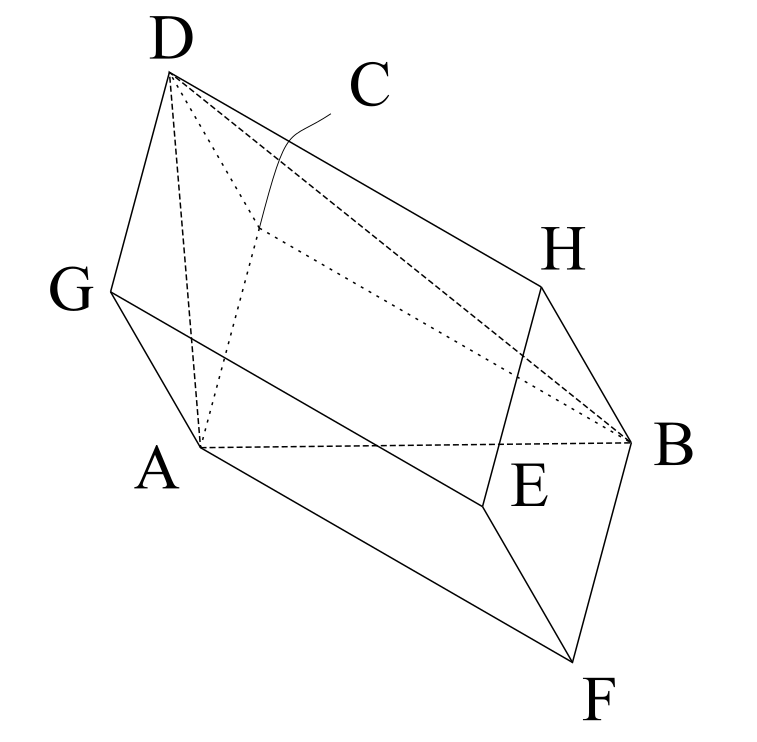
上の図において、この平行六面体の底面ACBFに対して、3点をとって三角形ABCとします。そして、その面に向かい合う面の一個を選んでその三角形につなげるだけで四面体の完成です。これが平行六面体に四面体を入れられる原理です。
先ほど平行六面体の体積の出し方を示しましたが、上記の性質を用いると四面体の体積をベクトル計算で出すことが出来るようになります。そしてその公式は(四面体の体積)=(それを含んでいる平行六面体の体積)÷6です。
上図でいえば、三角形ABCの面積は平行四辺形ACBFの面積の2分の1です。そして、三角錐の体積の公式から、三角錐ABC-Dの体積は三角柱ABC-GHDの体積の3分の1になりますから、これを掛け算して6分の1を得るわけです。
ところで、元の問題にて体積を求める立体は四角錐です。しかし四角錐は四角形になっている底面を2つの三角形に分割することで三角錐にすることができます。

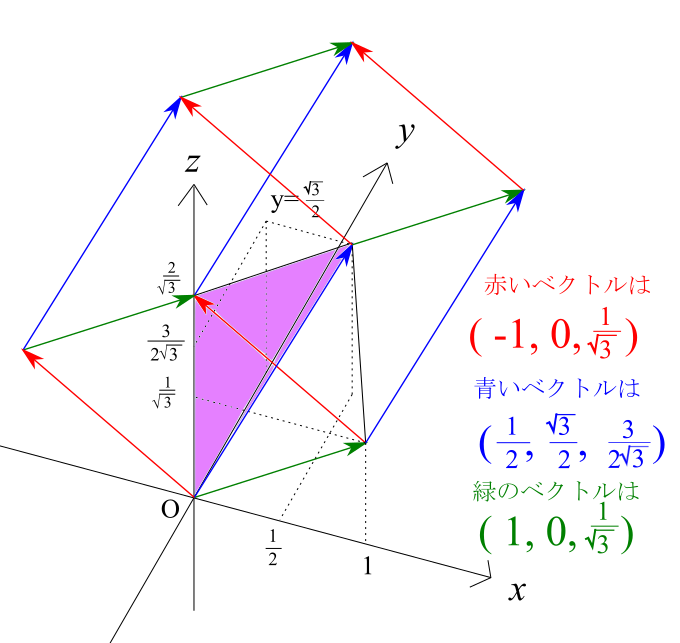
やり方として、上のように赤い線のところで底面を切ります。こうすることでそれぞれ紫色、水色の底面を持つ「三角錐2つ」にできます。
ただし、xyz座標軸は図示している配置の仕方を守る必要があります。これは座標系が通称「左手系」とよばれるものになり、外積の計算が変わってしまうためです。
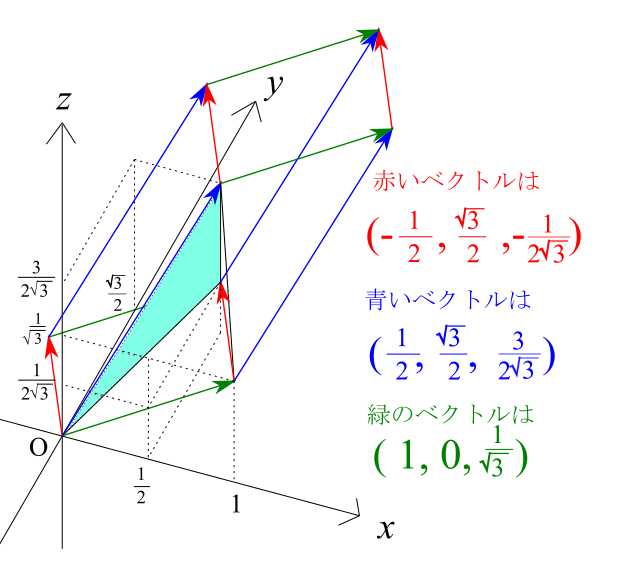
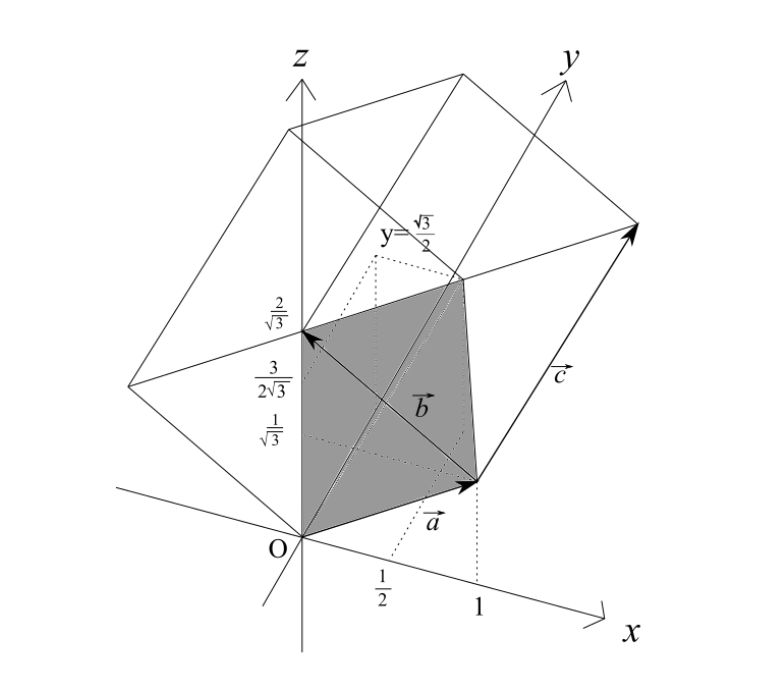
まずは赤線の下の部分、すなわち底面が水色の部分を切り出してこれを平行六面体に入れます。入れた結果が上の図です。平行六面体の各辺をベクトルとしてみれば、そのベクトルの種類は3つで尽くされます。
そしてここから、先ほど解説した外積計算で体積を求める手法を高校数学の範囲で収まるようにカモフラージュします。流れとしては、
- 平行四辺形の面積の公式で底面積を求める
- 底面をつくる2つのベクトルの外積を底面に垂直なベクトルとして「発見」する
- 2.の外積と平行四面体の残りの辺の間の余弦を求める
- 底面積に残りの辺の長さと3.で求めた余弦を掛けていく
- 4.の結果を6で割る
という流れです。このようにしないと減点の恐れがあるので必ず以上の流れを踏みましょう。答案に「外積」と書いたりベクトルを×でつないだりしないように注意してください。
1.の公式には2つの辺の間の角をθをおけばsinθが登場します。しかし内積で出てくるのはcosθ、一見して出せないように見えます。そのような場合には以下の変形をしましょう。

二乗の計算は面倒ですがこうすれば正弦でも問題なく計算できます。
次に2.ですがここが重要です。aとbの外積を出したらそれを外積であることを黙ってください。あくまで「aとbの両方に垂直なベクトルd」として扱ってください。文面だけでは何のことか分からないかもしれないので解答の一部を示します。
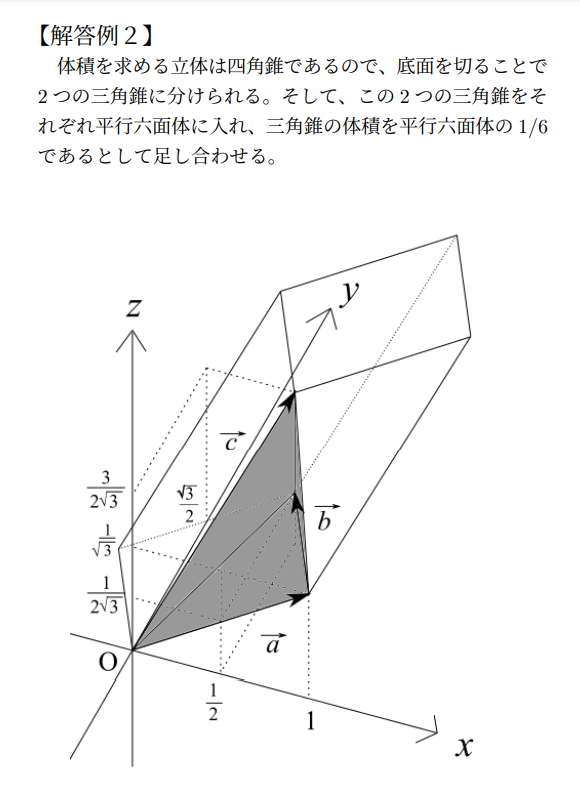


はい。これが「aとbに垂直なベクトルとして発見するd」です。dは元はといえばa×bなので当然aとbのどちらにも直交します。なんとも白々しい書き方ですがこれで通しましょう。
ちなみになぜ以上のやり方にする必要があるのかですが、これは「採点を大学レベルでさせないため」です。大学数学は高校数学の比にならない程定義にうるさく、採点基準も非常に厳しいものになります。
これを回避するためには解答には絶対に「外積」という言葉を使ってはならないのです。ベクトル同士を「×」で繋げることもNGです。
しかしこのような見え透いた嘘で許してくれるのか?と思われるかもしれません。それについてはご安心ください。数学的に合っていれば減点はありません。
長くなりましたがここから次のテクニックにいきます。次は先ほど求めたdとcの間の余弦を求めるところです。これは前章で取り上げたベクトル三重積の内積の部分です。特別に何か書くほどのことはありません。
これに底面積とベクトルcの絶対値をかけて体積を求めることも特に説明はいらないですね。最後に6で割ることをくれぐれも忘れないようにしましょう。では解答の続きをお見せします。

ここまでで下側の三角錐についての計算です。上側の場合も基本は同じになります。


計算自体は全て簡単なもので収まります。今回はわざわざ以上のような回りくどい解法を使わずとも解けますが、本番はどんな問題が出るか分かりません。
それこそ、外積の考え方を用いることで簡単になる問題が出る可能性さえもあります。たまには寄り道をして数学そのものへの理解を深めることも重要といえるでしょう。
数学の偏差値を上げるために
大切なこととは?
ここまで大阪大学の立体問題について解説してきました。表題の内容について率直な解答をすると、それは「様々な可能性を追い求めること」です。
筆者は昔小学校の先生に「算数が好きだ」と言うとその先生には「でも算数には答えが1つしかないよ」と言われました。こういう経験をした人は多いと思います。
今なら筆者は「そんなことはありません」と返します。逆に数学が好きな中高生がよく言う理由は「別解を探すのが楽しいから」なのですが、この別解の存在が同じ問題を全く違う姿に変えてしまうことだってあります。
その意味では今回の問題はそれが分かりやすいのではないでしょうか。簡単な積分計算だけで解く解法と、外積や平行六面体の知識を使って遠回りしながらも与えられた図形の特徴をフル活用して解く解法という、まったく対極にあるふたつの解答を見て頂きました。
そのための大学数学の話が少々長くなってしまいましたが、同じ問題でもまた違う切り口で見れば全く違って見られるところが数学の面白さです。
「好きこそものの上手なれ」と言います。皆さんも是非こうした「別の視点」を楽しんで数学の問題を解いていただければと思います。偏差値が少なくとも10は上がりますよ。
その楽しい旅のナビゲーターにおすすめなのが東大家庭教師友の会に属する学生家庭教師です。彼らはそうした「数学の旅人」としては先輩ながらも、数個しか歳が離れておらず、その距離の遠さをまったく感じることなく楽しんで数学を学ぶことができます。
大学受験を越えた先でも数学の勉強は続きます。是非、東大家庭教師友の会の先生と一緒に、一生モノの冒険をしてください!
大学入試の数学対策は
友の会の家庭教師で決まり!
友の会の3つのメリット
特に数学を頑張りたいあなたへ向けて我々友の会が提供できるメリットは大きく分けて以下の3つになります。まずは一度、お読みください。
①数学が大得意な先生が教えてくれる!
友の会には京大、東大、大阪大をはじめ40,000人以上の難関大生が在籍しています。それだけ多くの家庭教師がいますから、数学を大得意とし、その数学力で入試を勝ち上がった先生も多く紹介できます。
それだけではありません。友の会の家庭教師は全員採用率20%以下の厳しい審査を通過しています。そして、教師に希望する条件で細かく絞り込みができます。もし相性が悪いと感じられた際には教師を交代させていただくことも可能です。
②モチベーションを徹底管理!

東大家庭教師友の会の教師は、生徒様の学習が成果につなげられるように、授業以外にも充実した学習サポートを行なっております。
日頃の計算練習や苦手克服のための問題演習など、数学の勉強はとにかく時間のかかる地味な作業も多いです。そのような場面でもモチベーションを失ってしまわないよう、友の会の家庭教師が徹底的にサポート。お悩みにも親身になってお応えできます。
③かかる料金は5つだけ!
東大家庭教師友の会では、ご入会時に入会金が発生します。月々のお支払いは、コースに応じた授業料、交通費、学習サポート費の合算になります。
授業を受けた時間数に応じてご請求額は変わり、指導回数や時間を臨機応変に変更することが可能です。
他社の家庭教師とはどう違う?
次に、東大家庭教師友の会と他社の違いを紹介します。東大家庭教師友の会の家庭教師は他社の家庭教師と比べて、「生徒様にぴったりの家庭教師を派遣できる」こと、「質の高い授業をリーズナブルに受けられる」ことが大きなメリットです。具体的に見てみましょう。
①生徒様にぴったりの家庭教師!
家庭教師は生徒様との相性がすべてです。どれだけ指導能力の高い家庭教師であっても、生徒様との相性がよくなければ、その能力を十分に活かすことはできません。その点、友の会は安心です。東大家庭教師友の会は体験授業(初回無料)によって教師との相性をチェックでき、もし合わないと思った場合はいくらでもチェンジできます。
教師の条件は出身校や在籍大学など、細かい条件で事前に指定することができます。いつ指導して頂くかもご家庭様でご自由に決めて頂けます。また、東大家庭教師友の会は原則すべての案件に立候補制を採用しているので、どの先生も熱意に溢れています。
さらに、東大家庭教師友の会の最大の特徴は「全員学生家庭教師であること」です。これは、生徒様と相性のよい家庭教師が見つかりやすいことを示しています。生徒様と歳が近く、価値観や趣味を共有できる可能性がプロの家庭教師よりも高いのです。
同業他社の場合ですと、例えばプロ家庭教師は経験豊富ですが、歳は生徒様から離れており、委縮してしまうかもしれません。教師の在籍数が少ないところではそもそも生徒様に合う教師が見つからない可能性すらあります。そして、本来生徒様と教師の相性をチェックして頂く最もよい機会である体験授業にそれ専用の人材を派遣してくる業者もあるようです。この点には十分注意する必要があります。
②明瞭な料金制度・高いコスパ
友の会の授業は難関大所属の家庭教師による質の高いものでありながら、コスパよくご利用いただけます。なぜなら、友の会では広告宣伝費などの諸費を極力安く抑えているからです。さらに、ご家庭様から頂く料金の大部分が教師の給与となるシステムも確立していますので、給料が安いことが原因で教師が積極的な指導をしてくれない、といったこともございません。
また、東大家庭教師友の会では後払い制度を採用しています。さらに、月謝制ではなく、その月の指導日数および指導時間により料金を計算させて頂いています。これにより、毎月指導を受けた分だけ、確定後にお支払いして頂けるような仕組みを整えております。
東大家庭教師友の会は先ほども見て頂いたように料金体系をあらかじめ明示していますが、一度問い合わせるまで料金を明示してくれない業者もあります。同業他社との詳細な料金比較は【30社】家庭教師料金を徹底比較!をご参照ください。
以上の点から、東大家庭教師友の会は他社と比較してもなお信頼できる家庭教師サービスであることがご理解いただけたかと思います。
大学入試の数学対策におすすめの家庭教師
以下に紹介する家庭教師はすべて現役の大学生であり、合格経験をもとにした質の高い指導をすることができることを当会が認めた優秀教師です。もっと多くの家庭教師の情報を見たい方は教師情報検索からどうぞ。
 |
橋本先生 |
 |
||||||
| 教師番号 | 944674 |
 |
橋本先生 |
 |
||||||
| 教師番号 | 944674 |
| 所属大学 | 大阪大学医学部医学科 |
| 出身高校 | 金沢大学教育附属高等学校 |
| 指導期間 | 2026年4月まで |
| 指導科目 | [小]英語,国語,算数,社会,理科
[中]英語,国語,数学,社会,理科 [高]英語,文系数学,理系数学,物理,化学,日本史 |
| 意気込み | 勉強は面倒なものですが、同時にやりがいのある楽しいものでもあります。その楽しさに気付ける様な指導を心がけます。 |
 |
金山先生 |
 |
||||||
| 教師番号 | 922216 |
 |
金山先生 |
 |
||||||
| 教師番号 | 922216 |
| 所属大学 | 大阪大学基礎工学部 |
| 出身高校 | 安積高等学校 |
| 指導期間 | 2024年3月まで |
| 指導科目 | [小]英語,国語,算数,社会,理科
[中]英語,国語,数学,社会,理科 [高]英語,現代文,古文,漢文,文系数学,理系数学,物理,化学,日本史 |
| 意気込み | 生徒様の現状、目標到達のために必要なプロセスを分析、把握し、生徒様の学力向上に貢献いたします!一緒に頑張りましょう! |
 |
守谷先生 |
 |
||||||
| 教師番号 | 959162 |
 |
守谷先生 |
 |
||||||
| 教師番号 | 959162 |
| 所属大学 | 大阪市立大学医学部医学科 |
| 出身高校 | 北野高等学校 |
| 指導期間 | 2026年3月まで |
| 指導科目 | [小]英語,国語,算数,理科
[中]英語,国語,数学,理科 [高]英語,文系数学,理系数学,物理,化学 |
| 意気込み | 丁寧な指導を心がけます。具体的にはその指導内容が理解だけでなく生徒様自身の身につくように、生徒様に合わせた学習計画を共に立てていきたいです。よろしくお願い致します! |
料金
東大家庭教師友の会では、ご入会時に入会金が発生します。月々のお支払いは、コースに応じた授業料、交通費、学習サポート費の合算になります。
授業を受けた時間数に応じてご請求額は変わり、指導回数や時間を臨機応変に変更することが可能です。
お問い合わせはこちら
以上の阪大入試の数学の良問解説はいかがでしたか?友の会の家庭教師の指導に興味を持った方はまずは一度お問い合わせください。
以下は電話、およびWEB上でのお問い合わせのリンクになります。対面での指導を希望される方は派遣可能エリアをご確認の上、こちらからお申し込みください。
派遣可能エリア外にお住まいの方でも授業をお受けいただけるよう、オンライン指導もご用意しております。
「家庭教師は欲しい、でもコロナが怖い!」という方にもおすすめのオンライン指導をご希望の方は下記のリンク先をご覧ください。
他の入試数学の問題について見る
東京大学
円周率は3.05より大きい(2003年) ~ゆとり教育への挑戦状?~
初代・閻魔の唇問題(1954年) ~閻魔が笑えば赤門は開く~
京都大学
剰余と数値計算(1999年) ~自分の得点を自分で決められる?~
tan1°は有理数か?(2006年) ~史上”最短”の入試問題~
東京工業大学
数列を割り切る素数(1986年) ~答えはすぐに分かるけれど~
同様に確からしくない確率の問題(2008年) ~いびつなサイコロ~
一橋大学
円と放物線(1981年) ~引っ掛けポイントを見抜くには?~
大阪大学
体積を積分で求める(1999年) ~立体問題のセオリー~
公式の証明(2013年) ~公式は証明してから使おう・阪大編~
神戸大学
対数の応用問題(1998年) ~盲点の桁数、その攻略法~
三角形の面積(1977年) ~解けなかったら落ちる?~