画像の問題を見て「この問題は加法定理の証明そのものではないのか?」と思った方も多いかもしれませんが、これがどういうわけか東大入試の歴史に残る良問となっています。この記事ではこの問題がなぜ良問なのかということと、「公式を証明してから使わなければいけない理由」について説明します。
まずは画像の問題にじっくり当たって解いてみましょう。解けたら以下の解説を読んで合っているか確かめましょう。もちろん、まったく解法が見当がつかない、15分ぐらい考えてみたけどわからないといった場合でも下の解説に進んでかまいません。
目次
3.(2)の解答
なぜこの問題を取り上げるのか?
見ての通りこれは、検定済みの数学Ⅱの教科書には必ず掲載のあるほど基本的な数学の定理である、加法定理の証明問題です。なぜこのような基本的な問題を今回良問として取り上げているのか、それには明確な理由があります。
大学の数学の先生にとって最もショッキングな事実として、この公式を証明できる高校生は全国に5%もいません。みんな覚えるだけ覚えて、肝心の証明はスルーしています。実際、この問題が東大で出た時も正答率が僅かに2割しかなく、入学式で教員に怒られた、という話まであります。
このような出題をしたのは東大の入試作成者に、「今の高校生は加法定理を証明できない、この状況は非常に良くない」という認識があったからです。この程度の初歩的な公式が証明できなければ大学に上がってからの数学の勉強で苦しむことのは明らかなのに、多くの人が高校の段階でその証明を理解していなかったのです。
この記事を見ているあなたも似たような状況かもしれません。この問題は本来ならばサービス問題であり、裏を返せば解けなければ受からないはずの問題です。面倒くさい、時間がないといった理由でこうした公式の証明から目を背けるのはやめにして、一度「数学」そのものに対して真摯に向き合う必要があるでしょう。
この問題を解くために
必要な考え方
それでは気を取り直してこの問題の解き方を考えていきましょう。……とはいえ、これはすらすらできて欲しい問題です。それに加えて、この証明がすらすら出来る人は証明過程を丸覚えするといったことはしません。「要点だけ覚える」ことを意識すればド忘れを起こすことはないので、今回は証明の「要点だけ覚える」ことを学んでいただきたいと思います。これは数学の勉強はもちろん、入試そのものを攻略するうえでも大変重要になります。
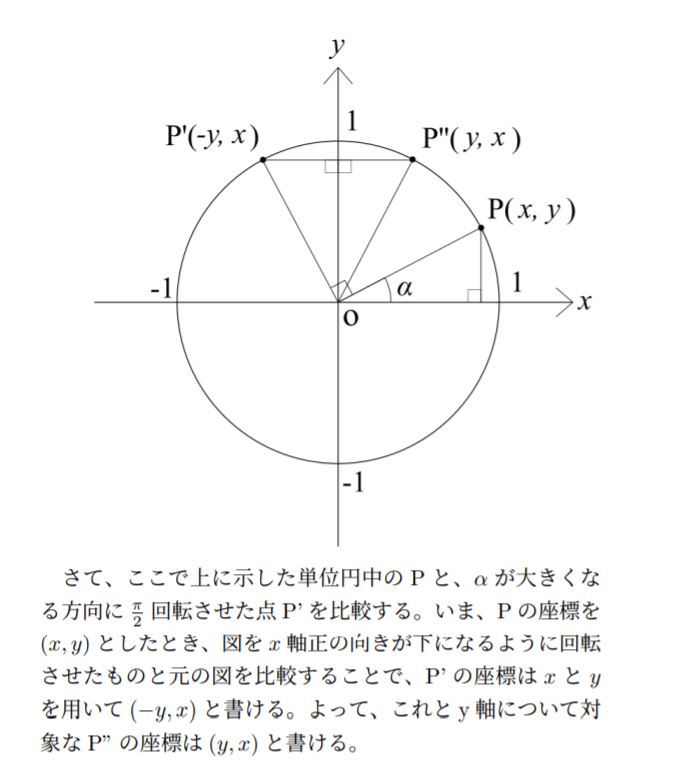
(1)は三角関数の定義です。「一般角に対して」定義するので、有効範囲が0°から90°までしかない直角三角形の方法では答えになりません。このため、高校数学の範囲ではおおよそ下に画像を示すやり方しかないと思われます。
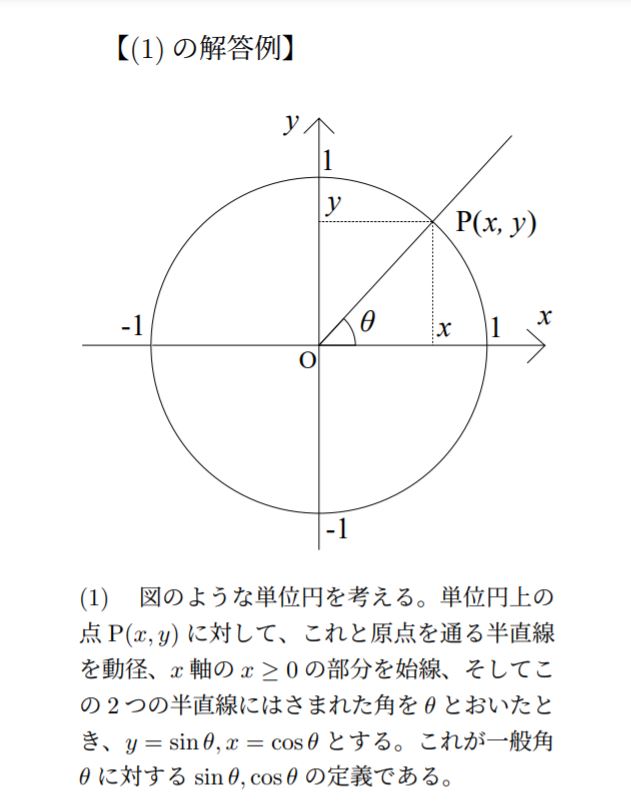
これで一般の角に対して定義をすることが可能になります。この他にはテイラー展開による定義や微分方程式による定義などがありますが、いずれも高校生には難しい内容です。
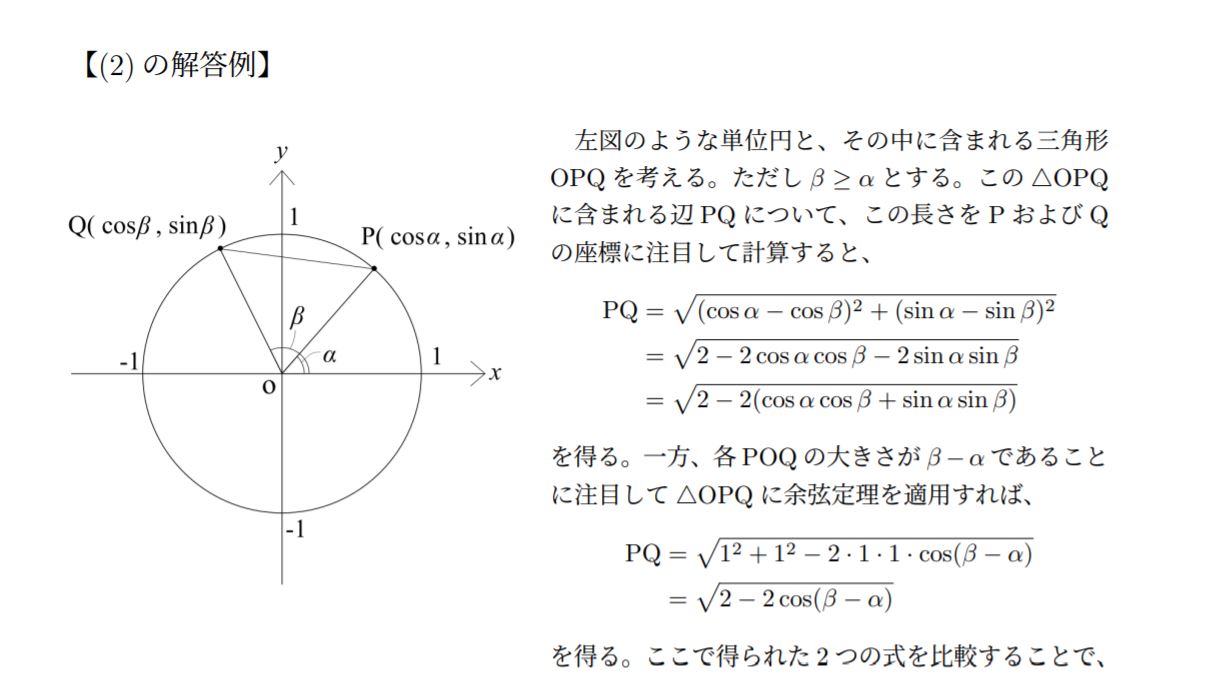
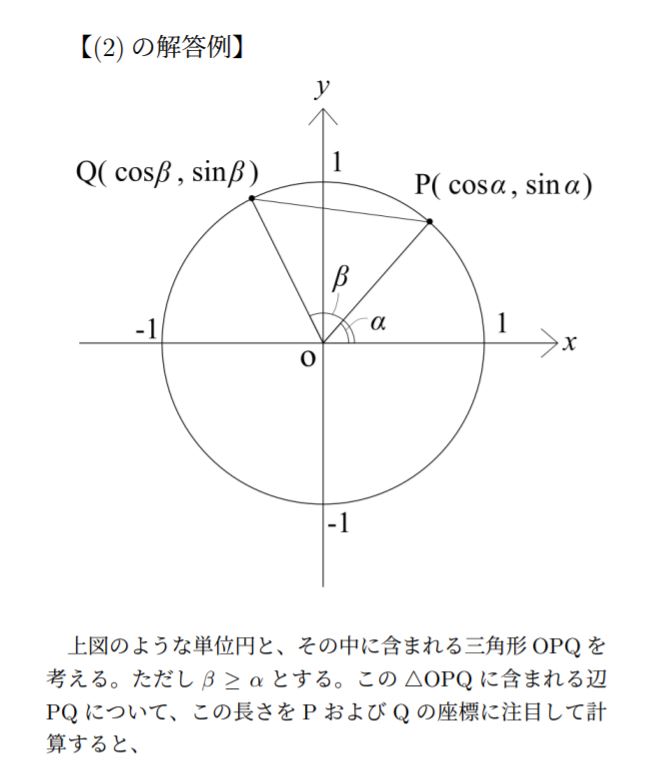
何はともあれ、これで(1)は解けました。ここからはこの(1)の結果をもとにして(2)を考えます。(1)で単位円による定義をしたので、(2)では単位円を証明に用いることになる、こう予想しておきましょう。まずは下に見える画像から考えてみます。
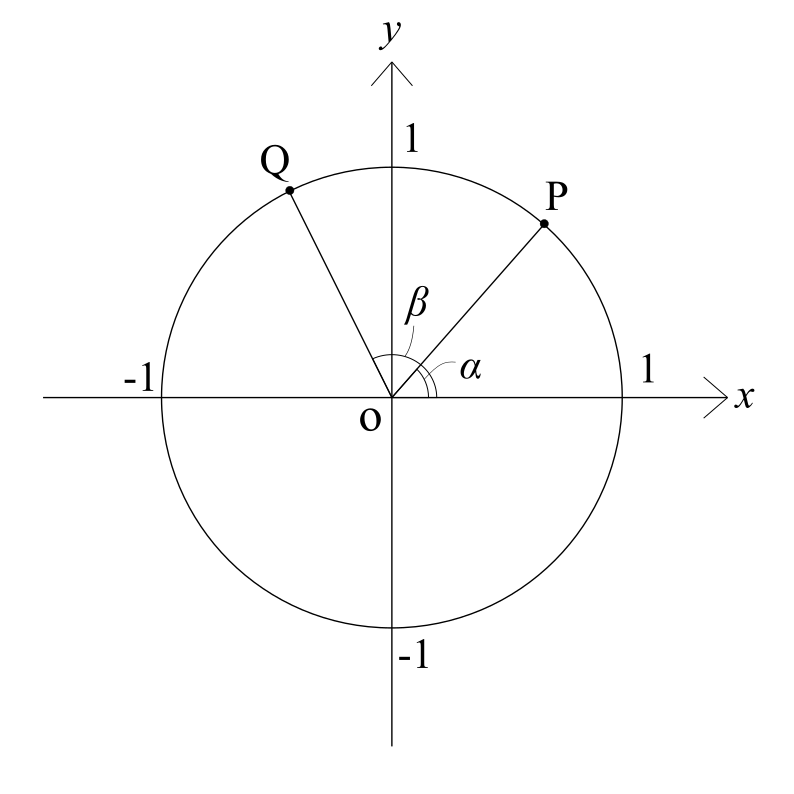
動径OP,OQが始線となす角がそれぞれα,βとなるように点P,Qを定めます。さて、ここからどうすればいいと思いますか?答えから言いますと、「PQの長さを2通りで表し、cos(β-α)についての式を作る」ことが必要になります。流石にこれを「思いつく」というのは無茶苦茶、というより天才の所業です。今回の証明の覚えるべき要点はここだけです。
というわけで、「ここにある情報だけでPQの長さを表す方法」を考えてみましょう。まず最初に、この図形がx-y平面上にあるから、PとQの座標はαとβを用いて表せて、そこからPQの長さを得られるのではないかということに気付くはずです。
実際にこれは、Pの座標が(cosα, sinα)で、Qの座標が(cosβ, sinβ)であることから、$$\rm{PQ^2}=(\cosα-\cosβ)^2+(\sinα-\sinβ)^2$$と表せます。もう1つのやり方は∠POQに注目して、ここから三角形POQの辺PQの長さを余弦定理で出すというものです。実際、$$\rm{PQ^2}=2-2\cos(β-α)$$となります。それではこれをもとに解答を書いてみましょう。
(2)の解答





数学Ⅰの三角比の単元で三角関数の変換公式を習ったかと思います。今回の解答ではこれも証明しておくことにしました。とはいえ、sinについての加法定理の使用を禁じられた環境下では図形による証明しか手段がないですし、なにより教科書に書いてあるやり方なので本番では省略しても減点はされないかと思います。むしろ、ここでは「数学の理論を構築する」にはどうすればいいのか、という点に注目していただきたいと思います。
それと、最初にβ>αとして証明を始めましたが、β<αの場合は示さずともよいです。αとβには対称性があるためです。この答案では最後に「βとαは入れ替えてもよい」と書くことで対称性があることを説明しています。
要点だけを覚えるということ
ここまで加法定理の証明を見てきました。一部の人はこれを覚えずに毎回導出するようですが、ほとんどの人には無理があろうかと思われます。そのため、とりあえず加法定理は覚えることとしますが、加法定理を覚えることで、以下に示す公式は全て30秒以内に導出することができます。
まずは倍角の公式です。正弦・余弦・正接の全3パターンを以下のように出すことができます。

正接は正弦を余弦で割ったものとして出すことになります。これを利用して、次は半角の公式を出してみましょう。導出はおおよそ次のようなやり方で行います。

さらに、積和の公式と和積の公式も以下に示すような方法で導出できます。一部のみ示すので、残りも同じ要領で出してみてください。積和の公式は全部で3種類、和積の公式は4種類存在します。

以上のように、倍角・半角・積和・和積の公式は試験本番中でも簡単に導出ができるわけですから、これをわざわざ語呂合わせなどを使って覚えるのはやめましょう。目安として、1分以内に証明できる公式を覚える必要はありません。これらを覚えるのに使っていた時間と脳みその容量は英語や古典などのどうしても暗記量を減らせない教科に回してください。
公式を証明できなければならない理由
最後に公式の証明の必要性についての話をして終わりにします。まず最初に言っておくべきことは、教科書の公式を丸暗記しているうちは初見の問題を解くことができない、ということです。
数学や物理学では意外な分野同士が手を結んでいることが多いです。これらの繋がりを受験生が知っていることを前提とした出題がなされることもあります。一つ一つの公式を個別に丸暗記しているようでは、こうした繋がりを見抜くことができないのです。
また、パターン学習で運よく大学入試を突破できたとしても、その後の勉強で地獄を見ることになります。大学で習う数学はとにかく論理を重視します。高校の段階では論理の厳密性を議論することはほとんどありませんでしたが、大学ではそれらを一つ一つ検証することになるのです。
そうなれば公式の丸暗記ではもはやどうしようもありません。一夜漬けで単位を取ることは出来ても肝心の講義内容は右から左で、受けた後の長期休暇を過ぎれば何も残っていないことに気付くはずです。それでは大学に行く意味はないでしょう。少なくとも、大学は単位を取るために行くところではないのです。
だからこそ、高校の段階で公式の証明からしっかりとやっておく必要があります。証明を通して一から理解した内容は忘れにくく、一生の財産になります。入試も大学の数学も、ここで土台をしっかり固めておけば圧倒的に楽になるのです。
そして、このような基本を身につけるにあたり、とても頼りになる助っ人が存在します。東大家庭教師友の会に所属する学生家庭教師です。採用率20%以下の厳しい審査を通過した難関大所属の家庭教師は数学の効果的な勉強法を熟知しており、なおかつ生徒様の目線に立った献身的な指導ができます。
ここからは当会所属の家庭教師だからできることを紹介していきます。私達東大家庭教師友の会は、大学入試の数学を攻略したい、第一志望校に合格したいというあなたの背中を全力で押します。
大学入試の数学対策は
友の会の家庭教師で決まり!
友の会の3つのメリット
特に数学を頑張りたいあなたへ向けて我々友の会が提供できるメリットは大きく分けて以下の3つになります。まずは一度、お読みください。
①数学が大得意な先生が教えてくれる!
友の会には京大、東大、大阪大をはじめ40,000人以上の難関大生が在籍しています。それだけ多くの家庭教師がいますから、数学を大得意とし、その数学力で入試を勝ち上がった先生も多く紹介できます。
それだけではありません。友の会の家庭教師は全員採用率20%以下の厳しい審査を通過しています。そして、教師に希望する条件で細かく絞り込みができます。また、相性が悪いと感じられた際には教師を交代させていただくことも可能です。
②モチベーションを徹底管理!

東大家庭教師友の会の教師は、生徒様の学習が成果につなげられるように、授業以外にも充実した学習サポートを行なっております。
日頃の計算練習や苦手克服のための問題演習など、数学の勉強はとにかく時間のかかる地味な作業も多いです。そのような場面でもモチベーションを失ってしまわないよう、友の会の家庭教師が徹底的にサポート。お悩みにも親身になってお応えできます。
③かかる料金は5つだけ!
東大家庭教師友の会では、ご入会時に入会金が発生します。月々のお支払いは、コースに応じた授業料、交通費、学習サポート費の合算になります。
授業を受けた時間数に応じてご請求額は変わり、指導回数や時間を臨機応変に変更することが可能です。
他社の家庭教師とはどう違う?
次に、東大家庭教師友の会と他社の違いを紹介します。ここでは大きく分けて「①派遣する教師」と「②料金」の2つに分けて解説していきます。
①派遣する教師の違い
まず、派遣する教師の違いについてです。友の会は採用率20%以下の厳しい審査を通過した優秀な難関大在籍の家庭教師を派遣しています。一方、他社は友の会のような学生家庭教師のみの会社もあればプロ家庭教師しか派遣しない会社もあり、さらにはその両方を派遣する場合もあったりと様々です。結局どこを選べばいいの?と思うかと思いますが、ここで重視すべき点はやはり「生徒様との相性」でしょう。
その点、友の会は安心です。友の会は体験授業(初回無料)によって教師との相性をチェックでき、もし合わないと思った場合はいくらでもチェンジできます。教師は全員学生なので生徒様と歳が近く、相性がいいことが多いですし、何より友の会には多くの教師が在籍していますから、生徒様に合う先生が選べる可能性はとても高いです。
一方、同業他社はどうでしょう?プロ家庭教師は経験豊富ですが、歳は生徒様から離れており、委縮してしまうかもしれません。教師の在籍数が少ないところではそもそも生徒様に合う教師が見つからない可能性すらあります。そして、本来生徒様と教師の相性をチェックして頂く最もよい機会である体験授業にそれ専用の人材を派遣してくる業者まであるという状況です。この点には十分注意する必要があります。
②料金制度の違い
次に料金に関してです。友の会の授業は難関大所属の家庭教師による質の高いものでありながら、その料金は家庭教師の市場においてはかなり安価な部類に入ります。なぜなら、友の会では広告宣伝費などの諸費を極力安く抑えているからです。さらに、ご家庭様から頂く料金の大部分が教師の給与となるシステムも確立していますので、給料が安いことが原因で教師が積極的な指導をしてくれない、といったこともございません。
それでは同業他社はどうかというと、まず適正な価格で指導をしてくれないところがあります。また、友の会は先ほども見て頂いたように料金体系をあらかじめ明示していますが、一度問い合わせるまで料金を明示してくれない業者もあります。料金関係でもっと問題なのが高額な教材販売を目的とする悪徳業者です。友の会ではそうした販売は一切行わず生徒様が既にお持ちのテキストなどで指導しますが、このような業者の存在が家庭教師の利用検討自体を難しくしているのです。
以上の点から、東大家庭教師友の会は他社と比較してもなお信頼できる家庭教師サービスであることがご理解いただけたかと思います。
大学入試の数学対策におすすめの家庭教師
以下に紹介する家庭教師はすべて現役の大学生であり、合格経験をもとにした質の高い指導をすることができることを当会が認めた優秀教師です。もっと多くの家庭教師の情報を見たい方はこちらからどうぞ。
 |
長澤先生 |
 |
||||||
| お問い合わせ番号 | 770839 |
 |
長澤先生 |
 |
||||||
| お問い合わせ番号 | 770839 |
| 所属大学 | 東京大学 |
| 出身高校 | 西大和学園高等学校 |
| 指導期間 | 2025年3月まで |
| 指導科目 | [小]国語,理科,社会,算数,英語
[中]国語,数学,理科,社会,英語 [高]化学,文系数学,物理,理系数学 |
| 意気込み | 自分の受験時代の経験を生かして、自分の弟と同じ年代の生徒様に勉強の楽しさを伝えて、生徒様自身も楽しく成績改善できるよう全力で頑張ります! |
 |
安藤先生 |
 |
||||||
| お問い合わせ番号 | 613009 |
 |
安藤先生 |
 |
||||||
| お問い合わせ番号 | 613009 |
| 所属大学 | 慶應義塾大学 |
| 出身高校 | 聖光学院高等学校 |
| 指導期間 | 2024年3月まで |
| 指導科目 | [小]理科,算数
[中]数学,理科,英語 [高]化学,文系数学,物理,理系数学,英語 |
| 意気込み | 明るく丁寧な指導を心掛けます! |
 |
三木先生 |
 |
||||||
| お問い合わせ番号 | 906560 |
 |
三木先生 |
 |
||||||
| お問い合わせ番号 | 906560 |
| 所属大学 | 東京大学 |
| 出身高校 | 横浜市立南高等学校 |
| 指導期間 | 2024年3月まで |
| 指導科目 | [小]国語,理科,社会,算数,英語
[中]国語,数学,理科,社会,英語 [高]化学,文系数学,物理,理系数学,英語 |
| 意気込み | 生徒様に寄り添い、丁寧な指導をしていけたらと思います。よろしくお願いします! |
料金
東大家庭教師友の会では、ご入会時に入会金が発生します。月々のお支払いは、コースに応じた授業料、交通費、学習サポート費の合算になります。
授業を受けた時間数に応じてご請求額は変わり、指導回数や時間を臨機応変に変更することが可能です。
お問い合わせはこちら
東大入試の加法定理の証明問題の解説はいかがでしたか?友の会の家庭教師の指導に興味を持った方はまずは一度お問い合わせください。
以下は電話、およびWEB上でのお問い合わせのリンクになります。対面での指導を希望される方は派遣可能エリアをご確認の上、こちらからお申し込みください。
派遣可能エリア外にお住まいの方でも授業をお受けいただけるよう、オンライン指導もご用意しております。
「家庭教師は欲しい、でもコロナが怖い!」という方にもおすすめのオンライン指導をご希望の方は下記のリンク先をご覧ください。
他の入試数学の問題について見る
東京大学
円周率は3.05より大きい(2003年) ~ゆとり教育への挑戦状?~
加法定理の証明(1999年) ~公式は証明してから使おう~
初代・閻魔の唇問題(1954年) ~閻魔が笑えば赤門は開く~
京都大学
剰余と数値計算(1999年) ~自分の得点を自分で決められる?~
tan1°は有理数か?(2006年) ~史上”最短”の入試問題~
東京工業大学
数列を割り切る素数(1986年) ~答えはすぐに分かるけれど~
同様に確からしくない確率の問題(2008年) ~いびつなサイコロ~
一橋大学
円と放物線(1981年) ~引っ掛けポイントを見抜くには?~
大阪大学
公式の証明(2013年) ~公式は証明してから使おう・阪大編~
神戸大学
対数の応用問題(1998年) ~盲点の桁数、その攻略法~
三角形の面積(1977年) ~解けなかったら落ちる?~