大阪大学入試の数学の過去の良問を徹底解説。本番に使える解き方も伝授します。

　画像の問題ふたつは2013年の大阪大学で出題された、入試業界でも有名な問題です。今回の記事では「この問題はどのように解けばいいのか」「数学の勉強において大切な姿勢は何か」を深掘りしていきます。

　まずは画像の問題にじっくり当たって解いてみましょう。解けたら以下の解説を読んで合っているか確かめましょう。もちろん、まったく解法が見当がつかない、15分ぐらい考えてみたけどわからない場合でも下の解説に進んでかまいません。

　また、今回は文系と理系で問題が分かれていますが、(文系の方はできればでよいので)両方の問題を解き、解説に目を通すことを推奨します。

目次

前半の問題を解くために
必要な考え方

　まずは前半、点と直線の距離の公式を証明する問題です。この公式自体は特に文系の人はお世話になることが多く、だからこそ「証明できないとは言わせないぞ」という強気の出題になっているといえます。

　実際この問題は解けなかったら落ちます。証明方法には座標によるものとベクトルによるものがあります。本番で出すなら特別な設定がいらない座標がおすすめです。

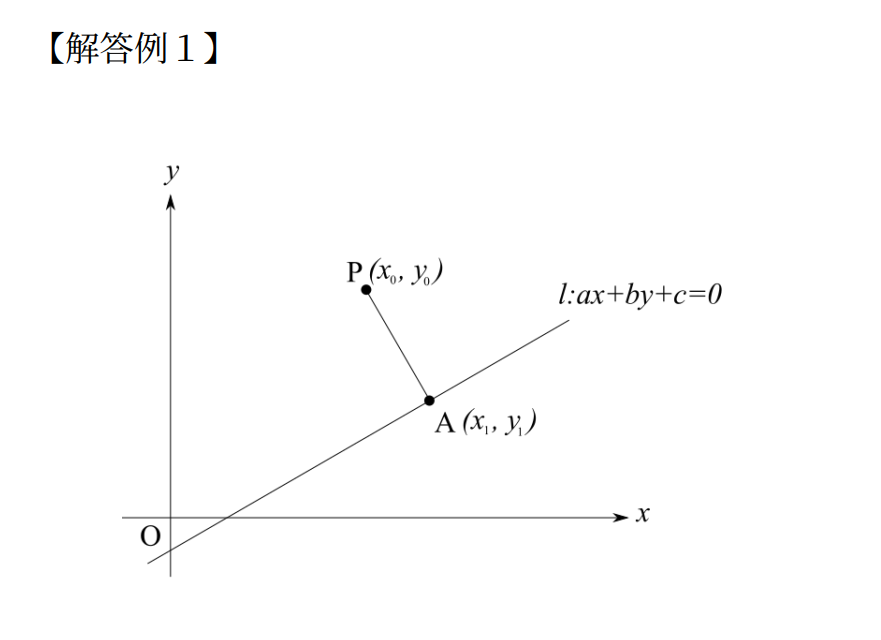
　まず、一般の直線l:ax+by+c=0と、その上にない点P(x0, y0)をおきます。そして、このPからlに向かって垂線を下ろし、その長さを求めるだけです。では解答を書きます。

前半の問題の解答

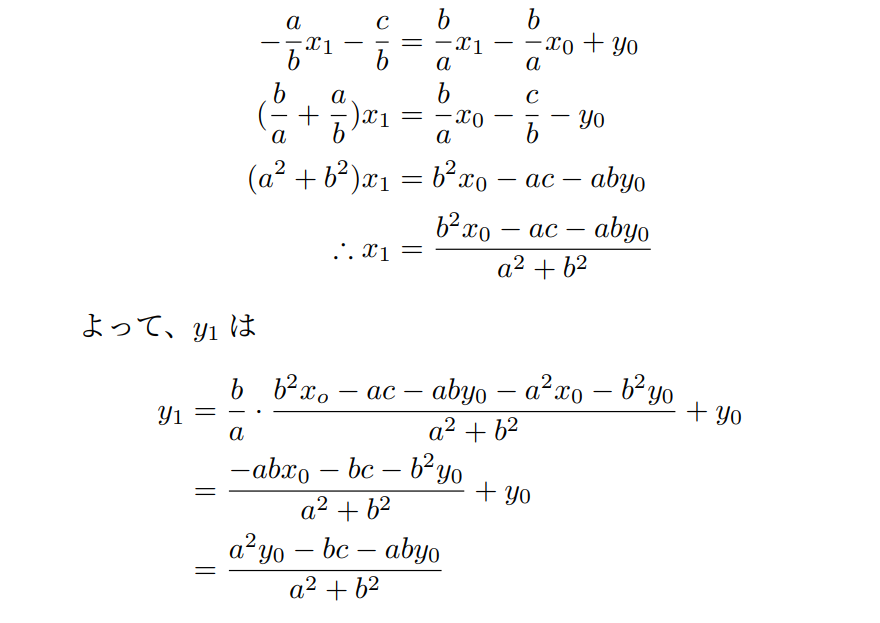
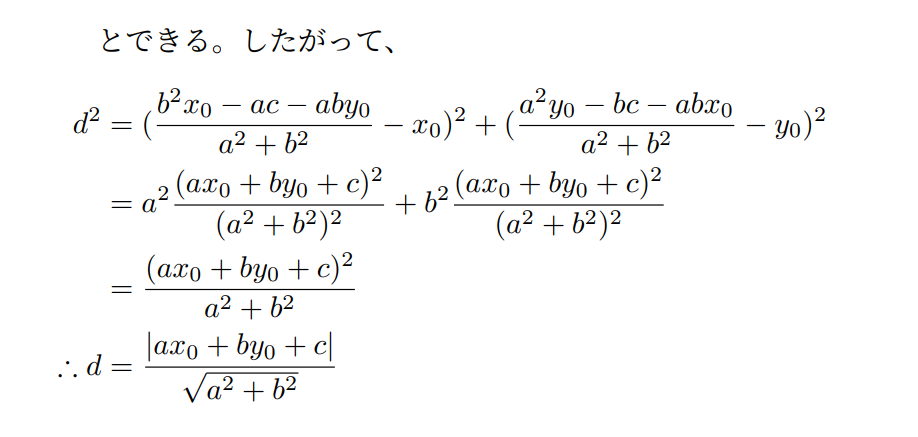
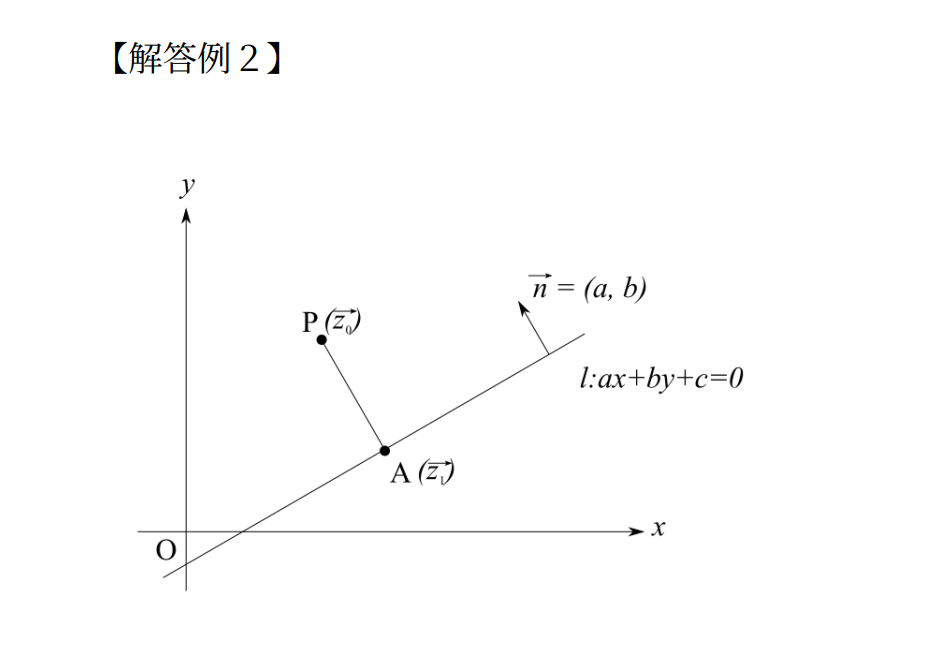
　後半はベクトルでの解答となります。座標を利用するものより計算量は少なく済みますが、初期設定を理解するのが大変で、本番でド忘れしてしまうかもしれません。(覚えているならば当然こちらでやるべきです。)

　補足として、法線ベクトルが(a,b)で与えられることについては直線lの傾きを考えればすぐに分かるかと思います。両方の解答とも、計算ミスには注意してください。

後半の問題を解くために
必要な考え方

　それでは後半戦に入りましょう。前半は受験生ならその場で出せて当然の証明でしたが、後半は若干話が変わってきます。なぜならば、これは高校の範囲では「完全な暗記問題」になっているからです。

　では、これから「暗記」するべき内容を書いていきます。まずは下の図を見てください。

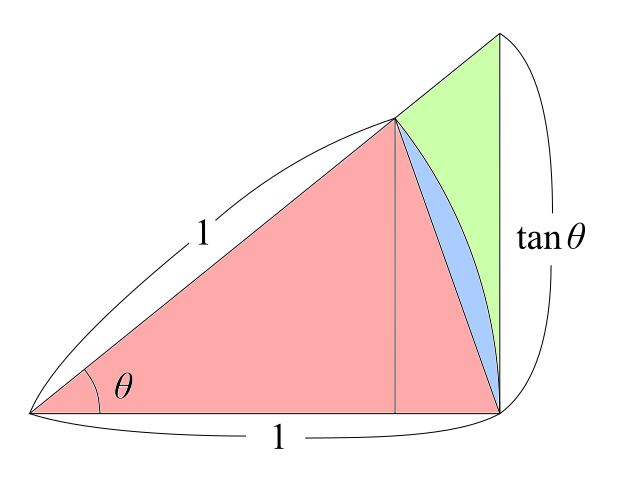
　図中の①「赤色の部分」、②「赤色＋青色の部分」、そして③「赤色＋青色＋緑色の部分」の面積を比較することを考えます。左からそれぞれS1,S2,S3とすると明らかにS1<S2<S3であり、さらに$$S_1=\frac{1}{2}\sin\theta, S_2=\frac{1}{2}\theta, S_3=\frac{1}{2}\tan\theta$$となります。この結果を先ほどの不等式に代入して変形し、はさみうちの原理を適用することで前半は証明できます。

　後半は微分の定義から考えてください。では解答を書きます。

後半の問題の解答と補足

　前半に証明したものを用いて後半を証明します。式変形は丁寧に行いましょう。しっかりとsinh/h→1を利用していることが採点者にわからないと大幅に減点されます。

　さて、ここまでの解答を書いておいて今更ではありますが、この証明方法には問題があると言われています。それは「循環論法に陥ってしまっている」という点です。

　循環論法とはいわゆる「悪魔の証明」で、A→Bであることを示すために用いるCが、実はBを前提にして示されているということなのです。今回の場合、面積比較でsinx/x→1を証明しましたが、この「面積比較」に問題があります。

　途中に扇形の面積が出ていたと思います。この扇形の面積を求めるために円の面積の公式S=πr^2を利用するのですが、実はこの公式は元はsinx/x→1を利用して示されているのです。それを具体的に見ていきましょう。

　ここまでしっかり数学という学問に真摯に向き合ってきた人なら、この段階で今回の問題の「危なさ」に気付けたと思います。円の面積は円周を用いた積分で出てきます。そして、その積分計算には三角関数の積分が現れます。

　積分は微分の逆として定義されています。そして、その「三角関数の微分」はsinx/x→1を前提として導出されているのです……！これが「循環論法」説の中身です。

　しかし、これはあくまでひとつの説です。ひょっとしたら良い逃げ道があるかもしれません。それは①円の面積を別の方法で求める方法と、②そもそも面積比較をsinx/x→1の証明に用いずにどうにかする方法です。

　以下はおまけのコーナーとしてこの2つの方法を考えていきます。解答の本筋には関係ありませんが、一応目を通しておくことをおすすめします。

①円の面積を別の方法で求める

　この主張は「円の面積を積分で出しているのが駄目なら積分によらない方法で円の面積を予め出しておけばよい」という内容の主張です。論証の危なさの回避方法としては順当なやり方といえるでしょう。

　まず、「正n角形はnを無限に大きくすると円になる」ということはなんとなく予想できますか？実はこれ、数学の世界では「公理」、すなわち「証明はしない(できない)がみんなが認めたこと」として通用しています。

　この公理を利用して円の面積を求めます。すなわち、あらかじめ半径rの円に内接する正n角形の面積を求めてから、これをn→∞とすればよいのです。

　そのために正n角形の面積を求める方法を考えます。まずは以下の図を見てください。

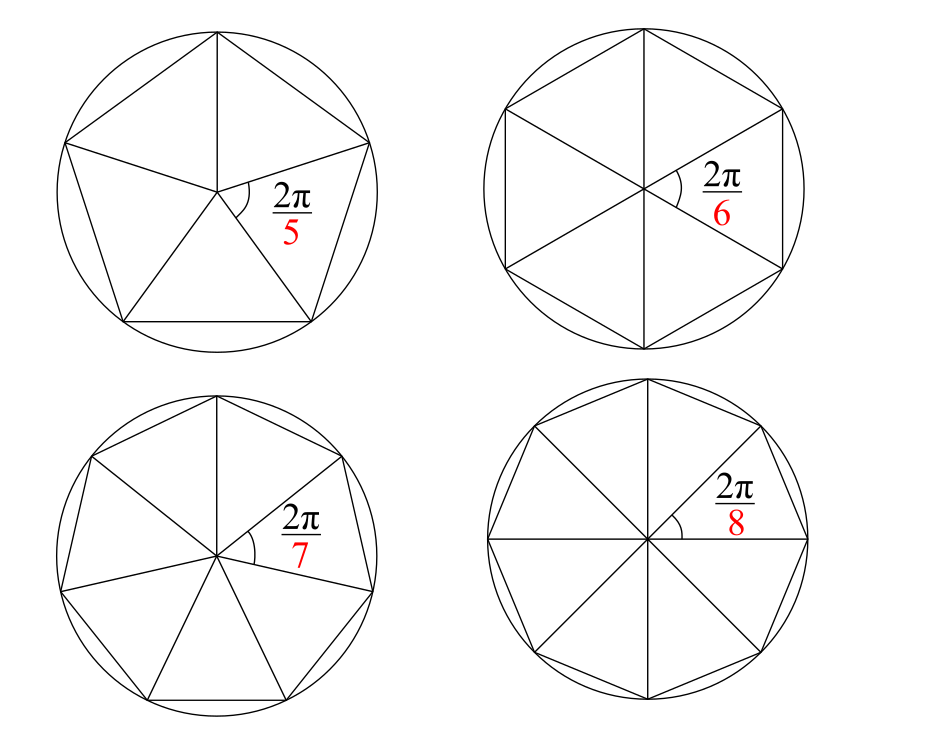
　円に内接する正五角形はその中心からすべての角に線分を引くことで、中心角を2π/5とする5つの二等辺三角形に分けることができます。正六角形の場合も同様にして中心角を2π/6とする6つの二等辺三角形に分けられます。

　このことを一般のnに適用すると、「円に内接する正n角形はその中心角を2π/nとするn個の二等辺三角形に分けられる」ことが成り立ちます。図では正七角形、正八角形の例も取り上げています。

　そして、二等辺三角形の大きさ2π/nの角を囲む辺の長さはどちらも円の半径rとなります。これを用いることで正n角形の面積を簡単に求めることができます。詳細は以下です。

　…ん？

　違和感に気付かれましたか？そうです。この証明は本来後から証明するはずのsinx/x→1を使ってしまっているので、これこそ循環論法になってしまいます。

　これ以外にも探せば円の面積の求め方はあるかもしれません。しかし、高校数学の範囲で出来るものはどれもsinx/x→1を使用してしまっているか、使用してはいないが厳密性に欠けているかのどちらかで、この矛盾から逃れられないのです……！

　そういうわけで①のアプローチは「詰み」ということにします。気を取り直して②のアプローチについて考察してみましょう。

②sinx/x→1の証明に円の面積を用いない

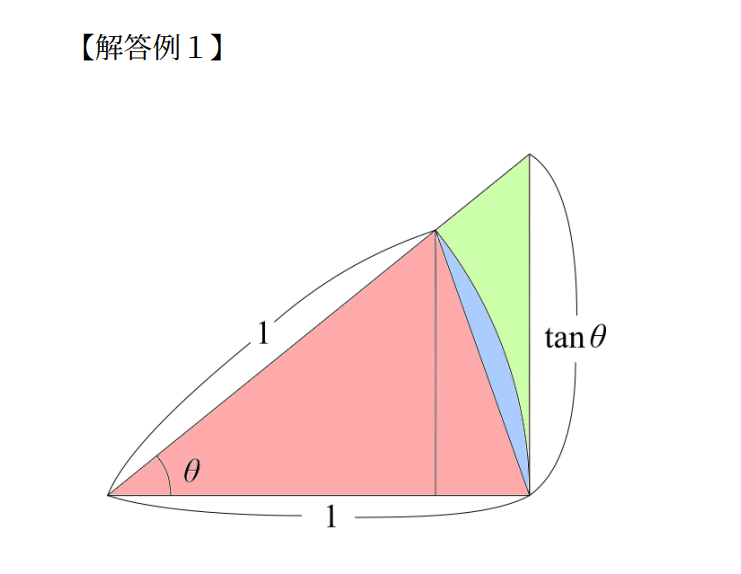
　図形の面積比較がダメな場合どうするか？辺の長さを比較します。もう一度先ほどの図を考えましょう。

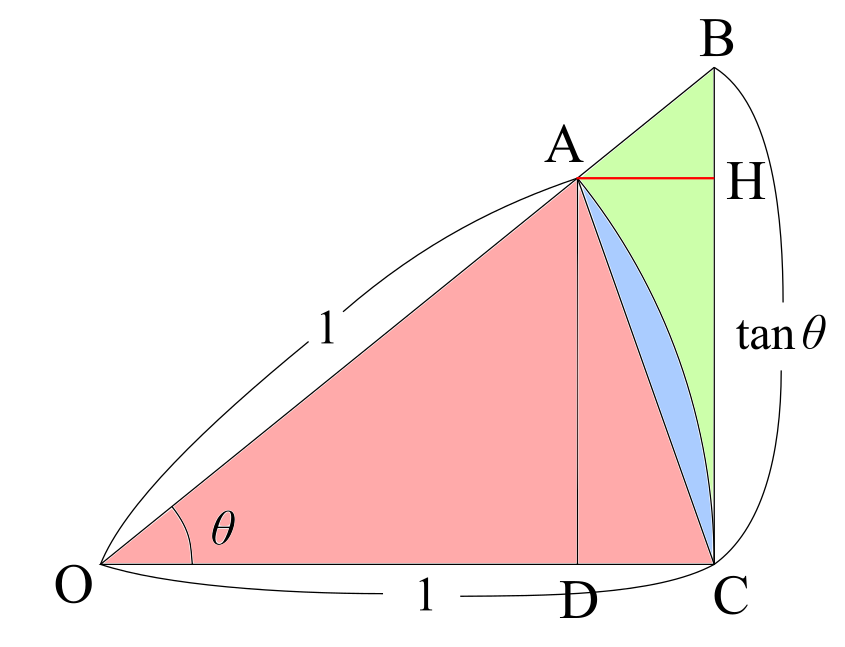
　考えやすくするために図に色々と手を加えました。辺の長さの比較ですが、ゴールは「sinθ/θ→1を示すこと」なので、「sinθ」または「θ」がその値に含まれる線分や曲線を探してはさみうちにすることになります。

　「θ」のほうで考えると、弧ACの長さがちょうどθなので、これをはさみうちにすればいけそうです。弧ACより短く、比較が容易な線分として弦ACがあります。そしてさらに線分ADは弦ACより短く、その長さはsinθです。

　これで弧ACの下限はどうにかなりそうなのですが、問題は上限です。弧AC<辺BCは常には成り立たないので、別の何かを探す必要があります。

　そこで考えるのが辺AH+HCです。こちらの長さは1-cosθ+sinθとすぐに求まりますし、見た目からして弧ACよりも長そうです。しかし、これは果たして本当に弧ACよりも長いのでしょうか？

　結論から言えばこれは弧ACよりも長いです。しかしその証明は若干特殊になります。以下、この証明も含めて実際に辺の長さを使うやり方でsinx/x→1を証明します。

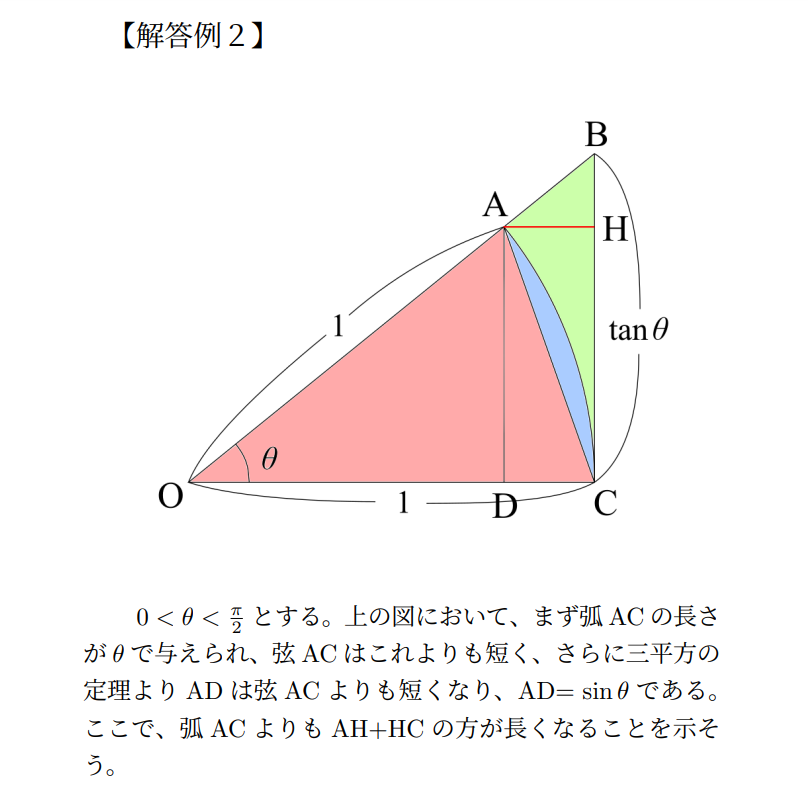
　解答内の説明が分かりにくいという方は以下の画像を見てください。

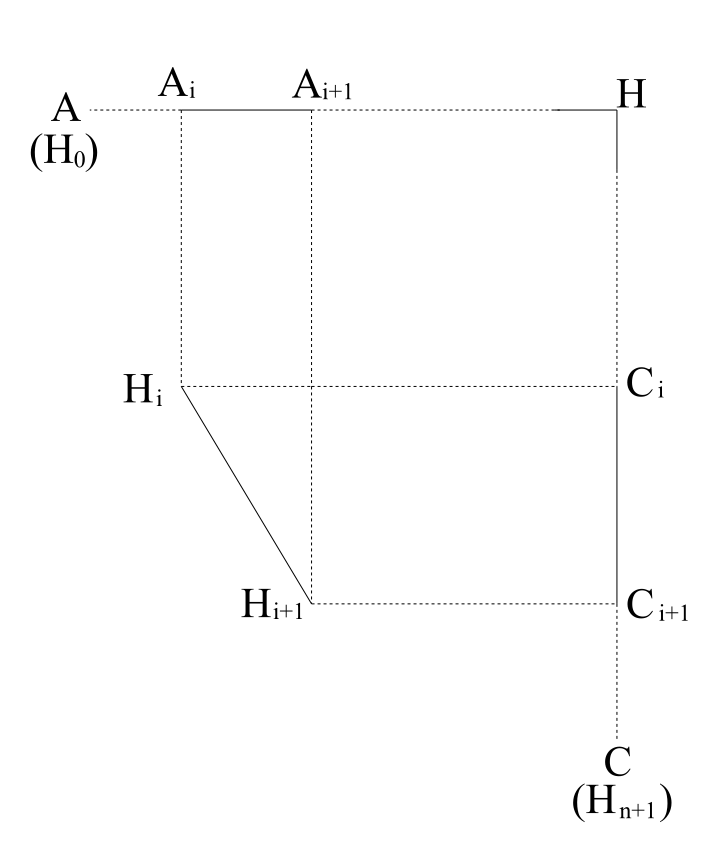
　画像には証明に出てきたA_i、A_i+1、C_i、C_i+1、H_i、H_i+1の位置関係を示しています。nを十分に大きくすれば刻みは非常に細かくなるので、本来は曲線である弧ACもそれを細断したものの個々は直線状であるとみなすことができます。

　H_i-H_i+1間が直角三角形の斜辺になり、なおかつ残りの2辺がそれぞれA_i-A_i+1およびC_i-C_i+1になることはわかりますか？三角形の各辺は元のA_i-A_i+1、C_i-C_i+1から平行移動しています。

　この3辺で三角形ができますから、後はその成立条件を利用して、iを0からnまで足し合わせておしまい、というわけです。一見難しそうですが内容自体は高校生でも十分理解できます。

　ただ、直角三角形の範囲内でcosθよりもcos^2θの方が小さい、ということはなかなか思いつかないと思います。大学入試でもあまり使わないテクニックではありますが、覚えておいて損はないでしょう。

　以上が「循環論法」の危険に対して高校数学の範囲内でギリギリ行える対処法になります。しかし、以上のような「完璧な」解答を書くところまでは出題者は期待していないでしょう。満点自体は教科書通りのやり方で貰えるはずです。

数学の偏差値を上げるために
大切なこととは？

　「偏差値」とは不思議な存在です。本来は生徒の学力を測るためのものさしの一種に過ぎないのに、こればかりが持てはやされて「目標」のひとつにまで押し上げられているのです。

　そして、「偏差値を上げること」はしばしば教育の世界では至上命題になります。しかし、これも「偏差値」の不思議な側面で、上げよう上げようと思っているうちはなかなか上がらず、上がっても一定のラインで打ち止めになってしまいます。

　その理由は簡単です。一般に使われる偏差値を上げるための「処方箋」は短期的なビジョンに基づくものであり、解法の丸暗記や典型出題への対策に終始してしまうため、なかなか学問の「本質」に到達できないからです。

　偏差値の「限界」を突破するための裏技はただひとつしかありません。基礎を完璧にし、「本質」が分かるようになることです。そしてその本質は数学の場合、基本的な定理や公式を全て自らの手で証明し、ひたすら問題を解き続けてようやく分かるものです。

　「数学の本質」を字面で説明するのは難しいでしょう。なぜなら、数理的な能力と言語的な能力は本来異なるものであるのに、それらは不可分であると我々は錯覚しているからです。そこには、試験ではこの2つの能力を一体にして運用すべきだという思い込みがあるのでしょう。

　以上が筆者の持論にはなりますが、要は「分かるようになるまではやるしかない」ということです。一見してぱぱっと公式を適用して終わりに見える数学ですが、実際には十分な修練なしには太刀打ちできない学問なのです。

　また、独学はかなり難しいです。これも数学のひとつの罠で、一見して参考書で独学することが正義に見えても、自分の間違いに自分で気づくことは誰にとっても難しく、これも数学の成績が上がらない要因になります。

　以上の問題に対するひとつの解決法として、筆者は東大家庭教師友の会に所属する現役難関大学生の家庭教師を薦めます。阪大のみならず東大・京大・東工大などにも多くの先生が在籍しており、数学を得意とする先生も多数所属しています。

　もちろん、学歴だけが優れるわけではありません。指導力・人間力ともにしっかりと担保されており、あなたの数学の勉強を精一杯サポートしてくれます。

大学入試の数学対策は
友の会の家庭教師で決まり！

友の会の3つのメリット

　特に数学を頑張りたいあなたへ向けて我々友の会が提供できるメリットは大きく分けて以下の3つになります。まずは一度、お読みください。

①数学が大得意な先生が教えてくれる！

　友の会には京大、東大、大阪大をはじめ40,000人以上の難関大生が在籍しています。それだけ多くの家庭教師がいますから、数学を大得意とし、その数学力で入試を勝ち上がった先生も多く紹介できます。

　それだけではありません。友の会の家庭教師は全員採用率20%以下の厳しい審査を通過しています。そして、教師に希望する条件で細かく絞り込みができます。もし相性が悪いと感じられた際には教師を交代させていただくことも可能です。

②モチベーションを徹底管理！

　東大家庭教師友の会の教師は、生徒様の学習が成果につなげられるように、授業以外にも充実した学習サポートを行なっております。

　日頃の計算練習や苦手克服のための問題演習など、数学の勉強はとにかく時間のかかる地味な作業も多いです。そのような場面でもモチベーションを失ってしまわないよう、友の会の家庭教師が徹底的にサポート。お悩みにも親身になってお応えできます。

③かかる料金は5つだけ！

かかるのは5つの料金のみ

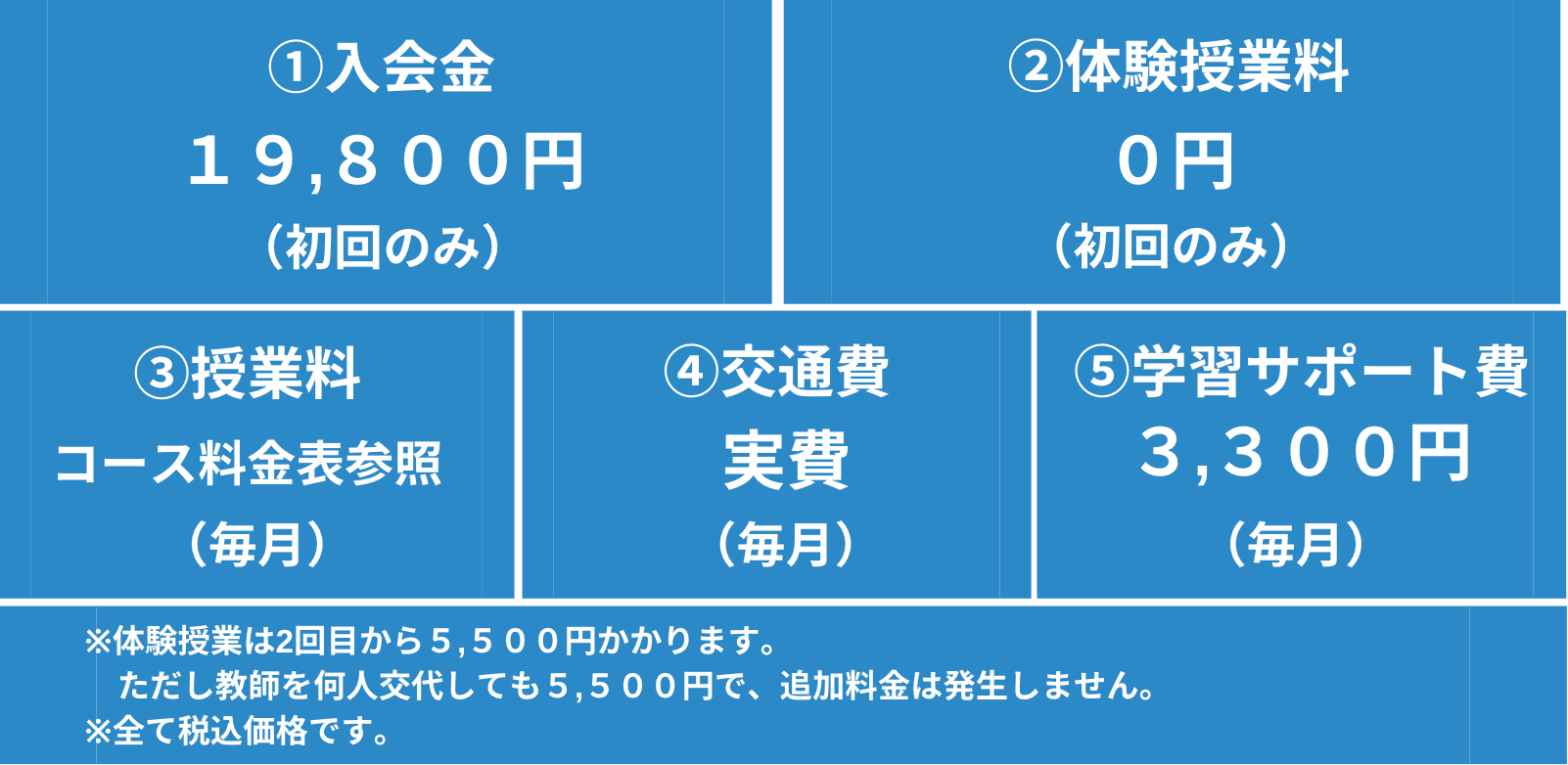
※体験授業に関して1回目は無料ですが、2回目以降は教師の交代料金として5,500円が発生します。しかし、何人受けても5,500円以上発生することはありません。

　友の会では、入会金・体験授業料（初回無料）・授業料・教師交通費・学習サポート費以外の料金はいただいておりません。よくある教材費などの料金はございませんのでご安心ください。ご家庭に安心してご利用していただけるよう適正かつ明確な料金体系を実現しております。

　友の会の家庭教師は他業者と比べてもリーズナブル。そのうえ、質の高い先生をご紹介できますから、親御さんにもきっとご満足いただけます。

他社の家庭教師とはどう違う？

　次に、東大家庭教師友の会と他社の違いを紹介します。東大家庭教師友の会の家庭教師は他社の家庭教師と比べて、「生徒様にぴったりの家庭教師を派遣できる」こと、「質の高い授業をリーズナブルに受けられる」ことが大きなメリットです。具体的に見てみましょう。

①生徒様にぴったりの家庭教師！

　家庭教師は生徒様との相性がすべてです。どれだけ指導能力の高い家庭教師であっても、生徒様との相性がよくなければ、その能力を十分に活かすことはできません。その点、友の会は安心です。東大家庭教師友の会は体験授業(初回無料)によって教師との相性をチェックでき、もし合わないと思った場合はいくらでもチェンジできます。

　教師の条件は出身校や在籍大学など、細かい条件で事前に指定することができます。いつ指導して頂くかもご家庭様でご自由に決めて頂けます。また、東大家庭教師友の会は原則すべての案件に立候補制を採用しているので、どの先生も熱意に溢れています。

　さらに、東大家庭教師友の会の最大の特徴は「全員学生家庭教師であること」です。これは、生徒様と相性のよい家庭教師が見つかりやすいことを示しています。生徒様と歳が近く、価値観や趣味を共有できる可能性がプロの家庭教師よりも高いのです。

　同業他社の場合ですと、例えばプロ家庭教師は経験豊富ですが、歳は生徒様から離れており、委縮してしまうかもしれません。教師の在籍数が少ないところではそもそも生徒様に合う教師が見つからない可能性すらあります。そして、本来生徒様と教師の相性をチェックして頂く最もよい機会である体験授業にそれ専用の人材を派遣してくる業者もあるようです。この点には十分注意する必要があります。

②明瞭な料金制度・高いコスパ

　友の会の授業は難関大所属の家庭教師による質の高いものでありながら、コスパよくご利用いただけます。なぜなら、友の会では広告宣伝費などの諸費を極力安く抑えているからです。さらに、ご家庭様から頂く料金の大部分が教師の給与となるシステムも確立していますので、給料が安いことが原因で教師が積極的な指導をしてくれない、といったこともございません。

　また、東大家庭教師友の会では後払い制度を採用しています。さらに、月謝制ではなく、その月の指導日数および指導時間により料金を計算させて頂いています。これにより、毎月指導を受けた分だけ、確定後にお支払いして頂けるような仕組みを整えております。

　東大家庭教師友の会は先ほども見て頂いたように料金体系をあらかじめ明示していますが、一度問い合わせるまで料金を明示してくれない業者もあります。同業他社との詳細な料金比較は【30社】家庭教師料金を徹底比較！をご参照ください。

　以上の点から、東大家庭教師友の会は他社と比較してもなお信頼できる家庭教師サービスであることがご理解いただけたかと思います。

大学入試の数学対策におすすめの家庭教師

　以下に紹介する家庭教師はすべて現役の大学生であり、合格経験をもとにした質の高い指導をすることができることを当会が認めた優秀教師です。もっと多くの家庭教師の情報を見たい方は教師情報検索からどうぞ。

			橋本先生

教師番号

944674

			橋本先生

教師番号

944674

所属大学

大阪大学医学部医学科

出身高校

金沢大学教育附属高等学校

指導期間

2026年4月まで

指導科目

[小]英語,国語,算数,社会,理科 [中]英語,国語,数学,社会,理科 [高]英語,文系数学,理系数学,物理,化学,日本史

意気込み

勉強は面倒なものですが、同時にやりがいのある楽しいものでもあります。その楽しさに気付ける様な指導を心がけます。

			金山先生

教師番号

922216

			金山先生

教師番号

922216

所属大学

大阪大学基礎工学部

出身高校

安積高等学校

指導期間

2024年3月まで

指導科目

[小]英語,国語,算数,社会,理科 [中]英語,国語,数学,社会,理科 [高]英語,現代文,古文,漢文,文系数学,理系数学,物理,化学,日本史

意気込み

生徒様の現状、目標到達のために必要なプロセスを分析、把握し、生徒様の学力向上に貢献いたします！一緒に頑張りましょう！

			守谷先生

教師番号

959162

			守谷先生

教師番号

959162

所属大学

大阪市立大学医学部医学科

出身高校

北野高等学校

指導期間

2026年3月まで

指導科目

[小]英語,国語,算数,理科 [中]英語,国語,数学,理科 [高]英語,文系数学,理系数学,物理,化学

意気込み

丁寧な指導を心がけます。具体的にはその指導内容が理解だけでなく生徒様自身の身につくように、生徒様に合わせた学習計画を共に立てていきたいです。よろしくお願い致します！

大学入試数学攻略のための指導コース

　大学入試の数学の攻略のための指導コースは以下の3種類がございます。より質の高い指導を希望される場合は、一番下の「プレミアム大学受験コース」のご利用をおすすめします。

大学受験準備コース
料金 (税込)	高1～高2…4,400円/時間 ※高3進級後（４月以降）も指導が行われる場合、コース料金は+550円が適用されます。
コース内容	大学受験を目指す高校1,2年生向けのコースです。大学受験を経験した教師が自身の経験を元に、計画的に指導を行います。
大学受験コース
料金 (税込)	高3,浪人生…4,950円/時間
コース内容	大学受験対策をご希望の方向けのコースです。大学受験を経験した教師だからこそ、受験のテクニックはもちろん、入試直前のメンタルケアまで行うことができます。
プレミアム大学受験コース
料金 (税込)	高1～高2…5,500円/時間 高3,浪人生…6,050円/時間 ※高2以前に指導を開始し、高3に進級後（４月以降）も指導が行われる場合、１時間あたりの料金は上記高3料金が適用されます。
コース内容	上記いずれかの条件に加え、当会で定めた条件をクリアした、指導経験が豊富な家庭教師をご希望の方向けのコースです。

お問い合わせはこちら

　以上の阪大入試の数学の良問解説はいかがでしたか？友の会の家庭教師の指導に興味を持った方はまずは一度お問い合わせください。

　以下は電話、およびWEB上でのお問い合わせのリンクになります。対面での指導を希望される方は派遣可能エリアをご確認の上、こちらからお申し込みください。

　派遣可能エリア外にお住まいの方でも授業をお受けいただけるよう、オンライン指導もご用意しております。

　「家庭教師は欲しい、でもコロナが怖い！」という方にもおすすめのオンライン指導をご希望の方は下記のリンク先をご覧ください。

他の入試数学の問題について見る